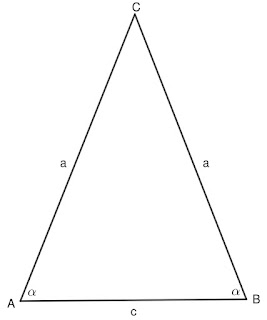
Височина, медиана и ъглополовяща към основата в равнобедрен триъгълник. Симетрала на отсечка 7 клас

Ще започнем този урок, като припомним някои важни теореми, които ще използваме в решаването на задачите. Теорема 1: В равнобедрен триъгълник височината, медианата и ъглополовящата към основата му съвпадат. Теорема 2: Ако в един триъгълник височината и медианата през един от върповете съвпадат, триъгълникът е равнобедрен. Теорема 3: Ако в един триъгълник височината и ъглополовящата през един от върховете съвпадат, триъгълникът е равнобедрен. Теорема 4: Ако в един триъгълник медианата и ъглополовящата през един от върховете съвпадат, триъгълникът е равнобедрен. Теорема 5: В равностранен триъгълник всички височини, медиани и ъглополовящи са равни. Определение 1: Права, която е пепендикулярна на дадена отсечка и минава през средата й, се нарича симетрала на тази отсечка. Симетралата на отсечката $AB$ ще отбелязваме с $s_{AB}$. Теорема 6: Всяка точка от симетралата на дадена отсечка е на равни разстояния от краищата на отсечката. Теорема 7: Всяка