Височина, медиана и ъглополовяща към основата в равнобедрен триъгълник. Симетрала на отсечка 7 клас

Теорема 1: В равнобедрен триъгълник височината, медианата и ъглополовящата към основата му съвпадат.

Теорема 2: Ако в един триъгълник височината и медианата през един от върховете съвпадат, триъгълникът е равнобедрен.

Теорема 3: Ако в един триъгълник височината и ъглополовящата през един от върховете съвпадат, триъгълникът е равнобедрен.

Теорема 4: Ако в един триъгълник медианата и ъглополовящата през един от върховете съвпадат, триъгълникът е равнобедрен.

Теорема 5: В равностранен триъгълник всички височини, медиани и ъглополовящи са равни.

Определение 1: Права, която е перпендикулярна на дадена отсечка и минава през средата й, се нарича симетрала на тази отсечка.

Симетралата на отсечката $AB$ ще отбелязваме с $s_{AB}$.

Теорема 6: Всяка точка от симетралата на дадена отсечка е на равни разстояния от краищата на отсечката.

Теорема 7: Всяка точка, която е на равни разстояния от краищата на дадена отсечка, лежи на симетралата на тази отсечка.

1 Задача: Триъгълникът $ABC$ е равнобедрен с основа $AB$ и отсечката $CH$ е негова височина. Точката $P$ е от отсечката $CH$. Докажете, че:

а) $AP=BP$; б) $\sphericalangle APC=\sphericalangle BPC$; в) $\sphericalangle BAP=\sphericalangle ABP$.

Решение а): По условие $\triangle ABC$ е равнобедрен, следователно $AC=BC$ и $\sphericalangle A=\sphericalangle B$. $CH$ е височина към основата $AB$ и според Теорема 1 тя е и медиана и ъглополовяща, откъдето (1) $AH=BH$ ($CH$ - медиана). От това, че $CH$ е височина следва, че (2) $\sphericalangle AHP=\sphericalangle BHP=90^{\circ}.$

Разглеждаме $\triangle AHP$ и $\triangle BHP$:

1) $AH=BH$ (от (1));

2) $PH$ - обща;

3) $\sphericalangle AHP=\sphericalangle BHP=90^{\circ}$ (от (2)),

Следователно $\triangle AHP\cong\triangle BHP$ по I признак, откъдето следва, че $AP=BP.$

Решение б): Тъй като $CH$ е ъглополовяща имаме, че (3) $\sphericalangle ACP=\sphericalangle BCP$.

Разглеждаме $\triangle APC$ и $\triangle BPC$:

1) $CP$ - обща;

2) $\sphericalangle ACP=\sphericalangle BCP$ (от (3))

3) $AC=BC$ ($\triangle ABC$ - равнобедрен),

Следователно $\triangle APC\cong \triangle BPC$ по I признак, откъдето $\sphericalangle APC=\sphericalangle BPC$.

Решение в): Това следва непосредствено от решението a), защото доказахме, че $\triangle AHP\cong\triangle BHP$, а в еднаквите триъгълници всички съответни ъгли са равни.

2 Задача: В равнобедрения $\triangle ABC$ ($AC=BC$), $\sphericalangle ACB=40^{\circ}$, а симетралата на $AC$ пресича $BC$ в точката $D$ и продължението на $AB$ в точка $E$. Намерете големината на $\sphericalangle BCE.$

Решение: Тъй като $\triangle ABC$ е равнобедрен, то $AC=BC$ и $\sphericalangle BAC=\sphericalangle ABC$. От $\sphericalangle BAC+\sphericalangle ABC+\sphericalangle ACB=180^{\circ}$ получаваме $\sphericalangle BAC+\sphericalangle ABC=140^{\circ}$, откъдето $\sphericalangle BAC=\sphericalangle ABC=70^{\circ}.$

Тъй като $EM$ лежи върху симетралата $s_{AC}$ следва, че $ME$ е височина и медиана в $\triangle AEC$ и според Теорема 2 $\triangle AEC$ е равнобедрен с $\sphericalangle EAC=\sphericalangle ACE=70^{\circ}$.

Така $\sphericalangle BCE=\sphericalangle ACE-\sphericalangle ACB=70^{\circ}-40^{\circ}=30^{\circ}$.

3 Задача: Симетралата на бедрото $BC$ на равнобедрения $\triangle ABC$ пресича другото бедро $AC$ в точка $P$. Ако периметърът на $\triangle APB$ е равен на $39$ $cm$ и $BC=17$ $cm$, то намерете страната $AB$.

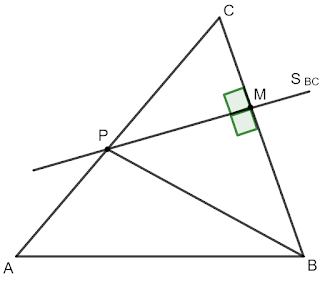
Решение: Нека симетралата $S_{BC}$ пресича $BC$ в точката $M$. Следователно $BM=MC$ и $PM\perp BC$ $\implies$ $PM$ е височина и медиана в $\triangle PBC$ и от тук следва, че $\triangle PBC$ е равнобедрен (това следва и от факта, че точката $P$ е от симетралата $S_{BC}$ и следователно $PC=PB$).

Нека $AP=x$. Тогава $PC=PB=17-x$. За периметъра на $\triangle ABP$ имаме:

$P_{\triangle ABP}=AP+AB+PB$ т.е. $39=AB+x+17-x$, откъдето $AB=39-17=22$ $cm$.

Задачи за самостоятелна работа

1. Върху бедрото $BC$ на равнобедрения $\triangle ABC$ съществува точка $D$ и тя е такава, че $CD=AD=AB$.

а) Намерете ъглите на $\triangle ABC$.

б) Докажете, че точка $D$ е на равни разстояния от правите $AB$ и $AC$.

2. В $\triangle ABC$ ($AC=BC$) симетралата на $BC$ пресича бедрото $AC$ в точка $M$, а симетралата на $CM$ пресича бедрото $BC$ в точка $N$. Докажете, че $\sphericalangle AMB=\sphericalangle MNB.$

3. Даден е $\triangle ABC$, в който $\alpha:\beta:\gamma=5:1:6$. Точката $M$ е средата на страната $BC$, а $H$ е пета на височината към $AB$.

а) Намерете големината на $\sphericalangle CMH$.

б) Докажете, че $AB=4CH$.

4. В $\triangle ABC$ ъглополовящата $AL$ разполовява медианата $CM.$

а) Докажете, че $AC=\frac{1}{2}AB$.

б) Намерете ъглите на $\triangle ABC$, ако $\sphericalangle BCM=30^{\circ}.$

Видео уроци

Още обяснени и решени задачи свързани с този урок можете да намерите в клипа ми даден по-долу:

Използвана литература:

1. Сборник за 7 клас, Пенка Рангелова, Константин Бекриев, Лилия Дилкина, Нина Иванова изд. Коала Прес, Пловдив, 2020

2. Тест Математика 7 клас, Донка Гълъбова, Адриана Хаджийска, Анна Аначкова и др., изд. Веди, София, 2020

3. Сборник задачи по математика за 7 клас, Мария Лилкова, Пенка Нинова, Таня Стоева и др., изд. Просвета, София

4. Книга за ученика за 7 клас, Здравка Паскалева, Мая Алашка, Райна Алашка, изд. Архимед, София, 2018

5. Текуща подготовка по математика за националното външно оценяване в 7 клас, Боянка Савова, Мария Тодорова, Веселин Златилов, изд. Просвета, София, 2020

6. Нови пробни изпити за външно оценяване и кандидатстване след 7 клас, изд. Регалия 6, София 2015

7. Тестове по математика, Любомир Любенов, Цеца Байчева, изд. DOMINO, 2017

8. Нови тематични и общи тестове по математика за 7 клас, Марина Рангелова, изд. Коала Прес, 2008

9. Учебно помагало за задължително избираема подготовка по математика за 7 клас, Иван Тонов, Таня Тонова, изд. Просвета, София, 2011

10. Тестове по математика за 7 клас, Лилия Дилкина, Константин Бекриев, изд. Коала Прес, Пловдив, 2014

11. Сборник контролни работи и тестове по математика 7 клас, Пенка Рангелова, изд. Коала Прес, Пловдив, 2009

12. Сп. Математика

13. Сп. Математика +