Средна основа (отсечка) на трапец 8 клас
Определение 1: Средна основа (отсечка) на трапец, ще наричаме отсечката, която съединява средите на бедрата на трапеца.
В сила са следните две теореми:
Теорема 1: Правата, която минава през средата на едното бедро на трапеца и е успоредна на една от неговите основи, разполовява и другото му бедро.
Теорема 2: Средната отсечка на един трапец е успоредна на основите му и е равна на полусбора им.
С други думи, ако имаме, че ABCD е трапец, в който AB\parallel CD и AM=MD, също така и BN=NC, тогава MN\parallel AB\parallel CD и освен това MN=\frac{AB+CD}{2}.
Нека да разгледаме следните няколко примера:
1 Задача Единият диагонал и едната основа на правоъгълен трапец са по 14 cm, а единият от ъглите му е 120^{\circ}. Да се намери средната основа на трапеца.
Решение:
Тай като \sphericalangle A=\sphericalangle D=90^{\circ} и \sphericalangle C=120^{\circ} (по условие) следва, че \sphericalangle B=60^{\circ}. Но по условие от AC=AB\implies \triangle ABC e равнобедрен триъгълник с ъгъл от 60^{\circ} от където можем да кажем, че \triangle ABC е равностранен и AC=AB=BC=14 cm (повече за равнобедрения и равностранен триъгълник може да намерите тук). Освен това \sphericalangle CAB=60^{\circ}\implies \sphericalangle CAD=30^{\circ}. Като приложим теоремата за катет срещу остър ъгъл от 30^{\circ} в правоъгълен триъгълник следва, че CD=\frac{1}{2}AC и CD=7 cm. Сега прилагаме формулата за средна основа в трапец т.е. MN=\frac{AB+CD}{2} и MN=\frac{14+7}{2}=10,5 cm.
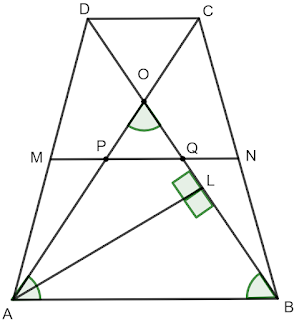
2 Задача Диагоналите на равнобедрен трапец ABCD (AB\parallel CD) се пресичат в точка O. Ъглополовящата на \sphericalangle OAB е перпендикулярна на BO. Ако AC=18 cm, намерете дължината на средната основа на трапеца
Решение:
Тъй като AL е ъглополовяща и AL\perp BO следва, че \triangle ABO е равнобедрен и AO=AB (триъгълник, в който ъглополовящата и височината към една от страните му съвпадат е равнобедрен триъгълник, може да се докаже, като се разгледат \triangle ALO и \triangle ALB и се докаже, че те са еднакви) и \sphericalangle AOB=\sphericalangle ABO. От това, че ABCD е равнобедрен трапец знаем, че \sphericalangle OAB=\sphericalangle OBA (от \sphericalangle A=\sphericalangle B и от \triangle ACD\cong \triangle BCD\implies \sphericalangle DAC=\sphericalangle CBD) следователно \triangle ABO има три равни ъгъла по 60^{\circ} и \sphericalangle OAL=\sphericalangle LAB=30^{\circ}. От тук можем да кажем и, че \triangle DOC също е равностранен и DO=CO=DC (\sphericalangle AOB=\sphericalangle DOC=60^{\circ} - връхни ъгли, \sphericalangle OAB=\sphericalangle OCD=60^{\circ} - кръстни ъгли и \sphericalangle OBA=\sphericalangle ODC=60^{\circ} - кръстни ъгли). Знаем, че средната основа MN=\frac{AB+CD}{2}. Нека MN\cap AC=P и MN\cap BD=Q. Сега да означим CO=CD=x, следователно AO=AB=14-x, тогава MN=\frac{14-x+x}{2}=7 cm.
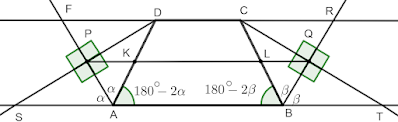
3 Задача В трапеца ABCD ъглополовящите на външните ъгли при върховете A и D се пресичат в точка P, а тези при върховете B и C - в точка Q. Докажете, че P_{ABCD}=2PQ.
Решение:
Нека \sphericalangle SAP=\sphericalangle PAD=\alpha, следователно \sphericalangle DAB=180^{\circ}-2\alpha (съседни ъгли). Аналогично \sphericalangle TBQ=\sphericalangle QBC=\beta и \sphericalangle ABC=180^{\circ}-2\beta (съседни ъгли). Така получаваме, че \sphericalangle ADC=2\alpha и \sphericalangle BCD=2\beta (това още може да се докаже, като се вземе в предвид, че \sphericalangle SAB=\sphericalangle ADC, като кръстни ъгли, аналогично и \sphericalangle TBC=\sphericalangle BCD). Така от тук имаме, че \sphericalangle ADP=\sphericalangle PDF=90^{\circ}-\alpha (от \sphericalangle ADC=2\alpha\implies \sphericalangle ADF=180^{\circ}-2\alpha - съсeдни ъгли) \implies \sphericalangle DPA=\sphericalangle DPF=90^{\circ} (DP - ъглополовяща). Аналогично \sphericalangle BCQ=\sphericalangle QCR=90^{\circ}-\beta\implies \sphericalangle CQR=\sphericalangle CQB=90^{\circ}. Така получаваме, че DP и CQ са височини и ъглополовящи, следователно \triangle FAD и \triangle RBC са равнобедрени и DF=DA, и CR=CB. Освен това точките P и Q са седи съответно на FA и BR (DP и CQ - медиани в равнобедрени триъгълници).
Тъй като \triangle SAP\cong \triangle DAP\implies SP=DP, аналогично \triangle CQB\cong \triangle BTQ\implies TQ=CQ \implies PQ е средна отсечка в трапеца STCD. Също така от PK\parallel FD и P - среда на FA\implies PK e средна отсечка в \triangle FAD и PK=\frac{1}{2}FD\implies PK=\frac{1}{2}AD. Аналогично QL - средна отсечка в \triangle BRC и QL=\frac{1}{2}CR\implies QL=\frac{1}{2}CB. Освен това от K и L - среди на AD и BC следва, че KL е средна отсечка в трапеца ABCD (виж Определение 1 от този урок) и KL=\frac{AB+CD}{2}. Така получаваме, че PQ= PK+KL+LQ=\frac{1}{2}AD+\frac{1}{2}AB+\frac{1}{2}CD+\frac{1}{2}BC следователно PQ=\frac{1}{2}P_{ABCD} т.е. P_{ABCD}=2PQ.
Задачи за самостоятелна работа:
1. Средната отсечка на един трапец е 16 cm. Единият от диагоналите му дели средната отсечка на части, разликата на които е 4 cm. Да се намерят основите на трапеца.
2. Даден е равнобедреният трапец ABCD (AB\parallel CD). Едното му бедро е 36 cm, а единият му диагонал разделя средната му основа на части съответно 12 cm и 30 cm. Да се намерят ъглите на трапеца.
3. Даден е равнобедрен трапец с остър ъгъл 60^{\circ} и средна отсечка 15 cm. Да се намерят страните на трапеца, ако средната му отсечка се разделя от диагоналите на три равни части.
4. Даден е равнобедреният трапец ABCD (AB\parallel CD) с взаимноперпендикулярни диагонали и средна основа, равна на 8 cm. Да се намери лицето на трапеца.
5. Даден е равнобедрен трапец ABCD (AB\parallel CD). Ъглополовящите на ъглите при бедрото AD се пресичат в точка M, а ъглополовящите на ъглите при бедрото BC - в точка K. Да се намери сборът на основите на трапеца, ако BC=10 cm и MK=4 cm.
6. Диагоналите на трапец образуват с голямата основа ъгли 60^{\circ}. Да се докаже, че средната отсечка на трапеца е два пъти по-малка от диагонала.
7. Диагоналите AC и BD на равнобедрения трапец ABCD се пресичат в точка O. Да се докаже, че ако AB е голямата му основа и \sphericalangle AOB=60^{\circ}, то средите на отсечките AO, DO и BC са върхове на равностранен триъгълник.
8. Единият от диагоналите и едната основа на правоъгълен трапец са по 14 cm, а единият от ъглите му е 120^{\circ}. Да се намери средната основа на трапеца.
9. Средната основа на равнобедрен трапец има дължина 5 cm, а малката основа - 2 cm, а лицето му е 15 cm^{2}. Намерете:
а) дължината на височината на трапеца;
б) ъглите на трапеца.
10. Върху бедрото AD на трапеца ABCD (AB>CD) са взети точки K и M, които го разделят на три равни части, като K е между A и M. През точките K и M са построени съответно прави k и m, успоредни на основите на трапеца, които пресичат диагоналите AC, BD и другото му бедро съответно в точките P, Q, L и T, R, N. Да се намерят дължините на малката основа, на отсечките от правите k и m, заключени между бедрата на трапеца, и на частите, на които те се делят от диагоналите му, ако се знаят дължините на голямата основа и на отсечката KP, съответно 21,6 cm и 3,6 cm.
Още решени и обяснени задачи може да намерите във видеото ми по-долу посветено на средната основа на трапец:





Коментари
Публикуване на коментар