Трапец. Равнобедрен и правоъгълен трапец 8 клас

Определение 1: Трапецът е четириъгълник, на който една двойка срещуположни страни са успоредни.

На чертежа имаме трапец $ABCD$ в който $AB\parallel CD$, като $AB=a>CD=b$. 

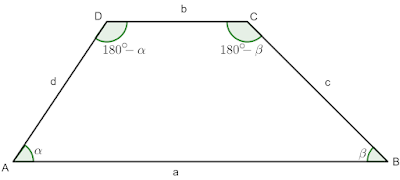
$AB$ - голяма основа;

$CD$ - малка основа;

$AD=d$ и $BC=c$ - бедра

За всеки трапец е изпълнени, че $\sphericalangle A+\sphericalangle D=\sphericalangle B+\sphericalangle C=180^{\circ}$, защото двойките ъгли $\sphericalangle A$ и $\sphericalangle D$, както и $\sphericalangle B$ и $\sphericalangle C$ са съответни ъгли и тъй като правите $AB$ и $CD$ са успоредни имат сбор от $180^{\circ}$.

По специалните видове трапци са:

1) Правоъгълен трапец

Определение 2: Трапец, на който едното бедро е перпендикулярно на основите му се нарича правоъгълен трапец.

$ABCD$ - правоъгълен трапец в който $AD\perp AB$ и $AD\perp CD$ и $\sphericalangle A=\sphericalangle D=90^{\circ}$. 

Тук $CH$ е височина в трапеца $ABCD$ и $CH=AD$, защото $AHCD$ е правоъгълник.

Можем още да кажем, че тъй като $AB=a$, $CD=b$ и от $AH=CD$ следва, че $HB=AB-CD=a-b$.

2) Равнобедрен трапец

Определение 3: Трапец, на който двете му бедра са равни се нарича равнобедрен трапец.

$ABCD$ - равнобедрен трапец, в който $AD=BC=c$.

В сила е следната теорема:

Теорема 1: Един трапец е равнобедрен, когато ъглите при една от основите му са равни.

Така от Теорема 1 имаме, че  $\sphericalangle A=\sphericalangle B=\alpha$ и $\sphericalangle C=\sphericalangle D=180^{\circ}-\alpha$.

В сила е още и следната Теорема 2:

Теорема 2: Един трапец е равнобедрен, когато диагоналите му са равни. 

Лицето на всеки трапец може да бъде пресметнато по формулата $S=\frac{(a+b)h}{2}$

1 Задача Даден е трапец $ABCD$ ($AB\parallel CD$) с пресечна точка на диагоналите $O$. Да се докаже, че ако $AO=OB$, то $ABCD$ е равнобедрен трапец.

Решение:

Тъй като $AO=BO\implies \triangle ABO$ е равнобедрен. Следователно $\sphericalangle OAB=\sphericalangle OBA=\alpha$. Освен това от $AB\parallel CD$ следва, че $\sphericalangle BAC=\sphericalangle DCO=\alpha$ (защото са кръстни ъгли, за да си припомниш виж тук) и $\sphericalangle ABO=\sphericalangle BDC=\alpha$. Така от тук имаме, че $\triangle DOC$ е равнобедрен и $DO=CO$. Така получаваме, че $AC=BD$ и следователно според Теорема 2 от днешният урок трапеца $ABCD$ е равнобедрен (трапец с равни диагонали).

2 Задача Острият ъгъл на един равнобедрен трапец е $60^{\circ}$. Диагоналите му са перпендикулярни на бедрата. Намерете периметъра на трапеца, ако бедрото му има дължина $5$ $cm$.

Решение:

От $AD=5$ $cm$ $\implies BC=5$ $cm$. Тъй като $\sphericalangle A=\sphericalangle B=60^{\circ}$ и $\sphericalangle ADB=\sphericalangle ACB=90^{\circ}$ $\implies$ $\sphericalangle DAC=\sphericalangle CAB=$ $=\sphericalangle DBC=\sphericalangle DBA=30^{\circ}$. Като приложим теоремата за катет срещу остър ъгъл от $30^{\circ}$ в правоъгълен триъгълник изучавана в $7$ клас имаме, че $AD=\frac{1}{2}AB$ т.е. $AB=10$ $cm$. Построяваме височините $DH$ и $CK$. Ясно е, че $\triangle AHD\cong\triangle BKC$ по $IV$ признак (виж тук) $\implies$ $AH=BK$. Като вземем в предвид, че $CD=HK$ ($HKCD$ - правоъгълник) $\implies$ $AH=BK=\frac{AB-CD}{2}$. Но като приложим теоремата за катет срещу остър ъгъл от $30^{\circ}$ в правоъгълен триъгълник за правоъгълния $\triangle AHD\implies$ $AH=BK=\frac{AD}{2}=2,5$ $cm$ $\implies$ $CD=AB-2AH=5$ $cm$. Тогава за периметъра имаме, че $P_{ABCD}=10+2.5+5=25$ $cm$.

3 Задача Даден е правоъгълен трапец $ABCD$ ($AB\parallel CD,\ AB>CD,\ AD\perp AB$). Лицето на $\triangle ABC$ е $\frac{2}{3}$ от лицето на дадения трапец. Да се докаже, че $\triangle ABC$ е равнобедрен.

Решение:

Нека да построим височината на трапеца $CH$.
От условието на задачата имаме, че $S_{\triangle ABC}=\frac{2}{3}S_{ABCD}$. Ясно е, че $S_{\triangle ABC}+S_{\triangle ACD}=S_{ABCD}$ следователно $S_{\triangle ABC}+S_{\triangle ACD}=\frac{3}{2}S_{\triangle ABC}\implies$ $\frac{3}{2}S_{\triangle ABC}+S_{\triangle ABC}=S_{\triangle ACD}$. От тук получаваме, че $S_{\triangle ACD}=\frac{1}{2}S_{\triangle ABC}$. За лицето на трапеца $ABCD$ имаме, че $S_{ABCD}=\frac{AB+CD}{2}.AD$ (вземаме в предвид, че височината на трапеца $CH=AD$, не бива да забравяме също така и, че $CH$ е височина в $\triangle ABC$). За лицето на правоъгълният $\triangle ACD$ имаме, че $S_{ACD}=\frac{AD.CD}{2}$. Сега като заместим в равенството $S_{ABCD}=\frac{3}{2}.2S_{\triangle ACD}\iff \frac{(AB+CD).AD}{2}=\frac{3AD.CD}{2}\iff$ $AB.AD+CD.AD=3AD.CD\iff AD(AB+CD)=3AD.CD\iff AB+CD=3CD\iff AB=2CD$. Тъй като $AH=CD$, защото $AHCD$ е правоъгълник $\implies AH=BH=CD$ и точката $H$ е среда на $AB$ следва, че $CH$ е медиана в $\triangle ABC$, но $CH$ е и височина в $\triangle ABC$ от където следва, че $\triangle ABC$ е равнобедрен и $AC=BC$.

4 Задача Бедрата на трапеца $ABCD$ (AB\parallel CD) са перпендикулярни и $AD=\frac{AB-CD}{2}$. Намерете ъглите на трапеца.

Решение:

От това, че $AD=\frac{AB-CD}{2}$ следва, че $2AD=AB-CD$.

 Построяваме права $DL\parallel BM$ и следователно $\sphericalangle ADL=90^{\circ}$ ($\sphericalangle ADL$ и $\sphericalangle DMB$ - съответни). Тъй като $AB-LB=AB-CD=AL$ получаваме, че $2AD=AL$. Така имаме, че катета $AD$ е два пъти по-голям от хипотенузата $AL$ и от теоремата за катет срещу ъгъл от $30^{\circ}$ следва, че $\sphericalangle ALD=30^{\circ}=\sphericalangle LBM$ и $\sphericalangle LAD=60^{\circ}$, $\sphericalangle LDC=30^{\circ}$ и $\sphericalangle DCB=150^{\circ}$, с което задачата е решена.

Задачи за самостоятелна работа:

1. Даден е равнобедрен трапец с периметър $78$ $cm$ и отношение на основите $11:5$. Намерете страните на трапеца, ако диагоналът му разполовява един от неговите ъгли.

2. В равнобедрения трапец $ABCD$ ($AB\parallel CD$) диагоналите $AC$ и $BD$ се пресичат в точката $O$ и $\sphericalangle AOB=60^{\circ}$. Да се докаже, че средите на отсечките $AO$, $DO$ и $BC$ са върхове на равностранен триъгълник.

3. В трапеца $ABCD$ ($AB\parallel CD$) от точките $D$ и $C$ са спуснати перпендикуляри към $AB$, които я пресичат съответно в точки $M$ и $N$. Ако $AD=2AM$ и $CN=BN$, намерете ъглите на трапеца.

4. В трапеца $ABCD$ основата $CD$ е $5$ пъти по-малка от основата $AB$ и точката $C$ лежи на симетралата на $AB$.

а) Докажете, че $S_{\triangle ABC}:S_{\triangle ABCD}=5:6$.

б) Ако $CD=2$ $cm$ и $P_{ABCD}=24$ $cm$, намерете периметъра на $\triangle ACD$.

5. Да се намери лицето на равнобедрен трапец с основи $20$ $cm$ и $14$ cm, ако един от ъглите му е $45^{\circ}$.

6. Даден е трапецът $ABCD$ с основи $AB$ и $CD$. През $C$ е прекарана права, успоредна на диагонала $BD$, която пресича правата $AB$ в точка $M$. Да се докаже, че:

а) триъгълниците $ACD$, $BCD$ и $BCM$ са равнолицеви;

б) лицето на триъгълника $AMC$ е равно на лицето на дадения трапец.

7. Да се намери лицето на трапец с диагонали $25$ $cm$ и $28$ $cm$ и ъгъл между диагоналите $150^{\circ}$.

8. Даден е трапецът $ABCD$. Върху правата $CD$ са дадени две точки $C_1$ и $D_1$ така, че $CD=C_1D_1$ и $ABC_1D_1$ е трапец. Да се докаже, че двата трапеца $ABCD$ и $ABC_1D_1$ са равнолицеви.

9. Даден е трапецът $ABCD$, диагоналите на който се пресичат в точка $O$. Да се докаже, че:

а) триъгълниците $ABC$ и $ABD$ са равнолицеви;

б) триъгълниците $ADO$ и $BCO$ са равнолицеви.

10. Даден е трапецът $ABCD$. Краищата на бедрото $BC$ са съединени със средата на бедрото $AD$. Да се докаже, че лицето на получения триъгълник е равно на половината от лицето на дадения трапец

11. Да се докаже, че пресечната точка на диагоналите на равнобедрен трапец е равноотдалечена от бедрата му.