Признак за еднаквост на правоъгълни триъгълници (IV признак). Ъглополовяща на ъгъл 7 клас

В началото на този урок ще припомним, някои важни теореми и дефиниции, които ще използваме при решаването на задачи от тази тема.

Теорема 1: Два правоъгълни триъгълника са еднакви, ако катет и хипотенуза от единия триъгълник са съответно равни на катет и хипотенуза от другия триъгълник.

Определение 1: Ъглополовяща на даден ъгъл се нарича лъчът с начало върха на ъгъла, който разделя този ъгъл на два равни ъгъла.

Теорема 2: Всяка точка от ъглополовящата на даден ъгъл се намира на равни разстояния от раменете на този ъгъл.

Теорема 3: Всяка точка от вътрешността на даден ъгъл, която е на равни разстояния от раменете му, лежи на ъглополовящата на този ъгъл.

1 Задача Докажете, че два равнобедрени триъгълника са еднакви, ако имат съответно равни бедра и височини към основата.
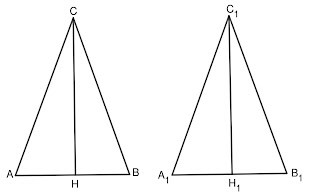
Решение:

Нека имаме два равнобедрени триъгълника (повече за равнобедрените триъгълници може да намерите тук) $ABC$ и $A_1B_1C_1$, в които $CH$ и $C_1H_1$ са височини. От условието на задачата имаме, че $AC=A_1C_1$, $BC=B_1C_1$ и $CH=C_1H_1$.
Разглеждаме правоъгълните триъгълници $AHC$ и $A_1H_1C_1$ (правоъгълни, защото $CH$ и $C_1H_1$ са височини).
1) $CH=C_1H_1$ (по условие);
2) $AC=A_1C_1$ (по условие), следователно $\triangle AHC\cong\triangle A_1H_1C_1$ по IV признак (според Теорема 1 от този урок), от където получаваме, че (1) $AH=A_1H_1$. Сега напълно аналогично разглеждаме $\triangle BHC$ и $\triangle B_1H_1C_1$
1) $CH=C_1H_1$ (по условие);
2) $BC=B_1C_1$ (по условие), следователно $\triangle BHC\cong\triangle B_1H_1C_1$ по IV признак (според Теорема 1 от този урок), от където получаваме, че (2) $BH=B_1H_1$. Сега от (1) и (2) имаме, че (3) $AB=A_1B_1$. Накрая разглеждаме $\triangle ABC$ и $\triangle A_1B_1C_1$
1) $AC=A_1C_1$ (по условие);
2) $BC=B_1C_1$ (по условие);
3) $AB=A_1B_1$ (от (3)),
следователно $\triangle ABC\cong\triangle A_1B_1C_1$ по III признак (повече за III признак може да намерите тук), с което задачата е решена.

2 Задача В триъгълник $ABC$ ъглополовящата на $\sphericalangle C$ пресича страната $AB$ в точка $D$ и височината от върха $A$ - в точка $E$. Намерете градусната мярка на $\sphericalangle BAC$, ако $AE=AD$.
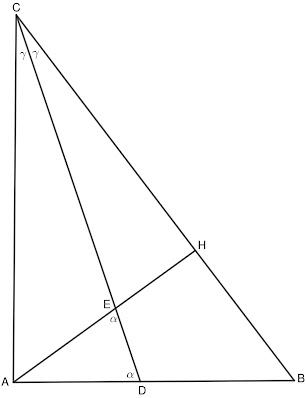
Решение:

Нека $AH$ е височината спусната от върха $A$ към страната $BC$. Следователно $\sphericalangle AHB=\sphericalangle AHC=90^{\circ}$. От това, че $CD$ е ъглополовяща имаме, че $\sphericalangle ACD=\sphericalangle BCD=\gamma$. Освен това в условието на задачата ни е казано, че $AE=AD$, от където следва, че $\triangle ADE$ е равнобедрен и $\sphericalangle AED=\sphericalangle ADE=\alpha$, така получаваме, че $\sphericalangle EAD-180^{\circ}-2\alpha$ (прилагаме теоремата за сбор на ъгли в триъгълник, повече за нея тук). Ъглите $ADC$ и $BDC$ са съседни, следователни $\sphericalangle BDC=180^{\circ}-\alpha$ (прилагаме теоремата за съседни ъгли, повече за нея тук). Така сега от правоъгълният $\triangle AHB$ имаме, че $\sphericalangle ABH=180^{\circ}-(90^{\circ}+180^{\circ}-2\alpha)=2\alpha-90^{\circ}$. От друга страна от $\triangle BDC$ за $\sphericalangle CBD=180^{\circ}-(180^{\circ}-\alpha+\gamma)=\alpha-\gamma$. Тъй като обаче $\sphericalangle ABH$ и $\sphericalangle CBD$ са един и същи ъгъл приравняваме получените две стойности за него, т.е. $\alpha+\gamma=2\alpha-90^{\circ}$, от където намираме, че $\alpha+\gamma=90^{\circ}$. Нека сега разгледаме триъгълникът $ADC$, за него имаме, че $\sphericalangle DAC+\alpha+\gamma=180^{\circ}$ и следователно $\sphericalangle DAC=180^{\circ}-90^{\circ}=90^{\circ}$, с което задачата е решена.

Задачи за самостоятелна работа

1. Равнобедрения $\triangle ABC$ има основа $AB=c$ cm и $\sphericalangle C=120^{\circ}$. Точката $M$ лежи на основата $AB$, като $AM:MB=1:2$.
а) Да се намери $CM$.
б) Докажете, че височината в $\triangle ABC$, спусната от върха $A$, е 3 пъти по-голяма от височината в $\triangle AMC$, спусната от върха $M$.

2. В $\triangle ABC$ $a:b:c=3:4:5$ и $P_{\triangle ABC}=48$ cm. Ъглополовящите $AA_1$ и $BB_1$ се пресичат в точката $O$, като разстоянието от нея до страната $AB$ е $4$ cm. Намерете лицето на $\triangle AOC$.

3. Даден е $\triangle ABC$, на който ъглополовящата на $\sphericalangle A$ пресича страната $BC$ в точката $N$. На най-голямата страна $AC$ е взета вътрешна точка $L$ така, че $\sphericalangle LNC=\sphericalangle BAC$. Да се докаже, че $NL=NB$.

4. В правоъгълния $\triangle ABC$ е построена височината $CH$, като $H\in AB$ към хипотенузата $AB$. Ъглополовящите $AL$ ($L\in BC$) на $\sphericalangle BAC$ и $CM$ ($M\in AB$) на $\sphericalangle ACH$ се пресичат в точка $O$. Докажете, че $O$ е средата на отсечката $CM$.

Още обяснени и решени задачи свързани с този урок можете да намерите в долното видео:

Използвана литература:

1. Сборник за 7 клас, Пенка Рангелова, Константин Бекриев, Лилия Дилкина, Нина Иванова изд. Коала Прес, Пловдив, 2020

2. Тест Математика 7 клас, Донка Гълъбова, Адриана Хаджийска, Анна Аначкова и др., изд. Веди, София, 2020 

3. Сборник задачи по математика за 7 клас, Мария Лилкова, Пенка Нинова, Таня Стоева и др., изд. Просвета, София

4. Книга за ученика за 7 клас, Здравка Паскалева, Мая Алашка, Райна Алашка, изд. Архимед, София, 2018

5. Текуща подготовка по математика за наицоналното външно оценяване в 7 клас, Боянка Савова, Мария Тодорова, Веселин Златилов, изд. Просвета, София, 2020

6. Нови пробни изпити за външно оценяване и кандидатстване след 7 клас, изд. Регалия 6, София 2015 

7. Тестове по математика, Любомир Любенов, Цеца Байчева, изд. DOMINO, 2017

8. Нови тематични и общи тестове по математика за 7 клас, Марина Рангелова, изд. Коала Прес, 2008

9. Учебно помагало за задължително избираема подготовка по математика за 7 клас, Иван Тонов, Таня Тонова, изд. Просвета, София, 2011

10. Тестове по математика за 7 клас, Лилия Дилкина, Константин Бекриев, изд. Коала Прес, Пловдив, 2014

11. Сборник контролни работи и тестове по математика 7 клас, Пенка Рангелова, изд. Коала Прес, Пловдив, 2009

12. Сп. Математика

13. Сп. Математика +