Квадрат 7 клас
Квадрат - дефиниции, свойства и задачи
Определение 1: Правоъгълник с две равни съседни страни се нарича квадрат.
Определение 2: Ромб с прав ъгъл се нарича квадрат.
Свойства на квадрата
Важно: Квадратът притежава всички свойства на:
Решени задачи
Задача 1: Нека ABCD е квадрат, в който диагоналите AC и BD се пресичат в точката O. Ако разстоянието от O до AB е 7 cm, намерете периметъра и лицето на квадрата ABCD.
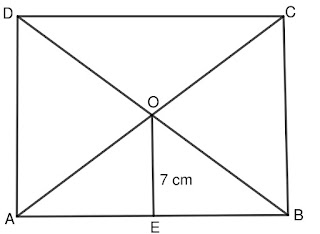
Решение:
1. Разстоянието от O до AB е OE = 7 cm
2. В квадрата диагоналите са равни и се разполовяват, следователно AO = BO = CO = DO
3. Триъгълник AOB е равнобедрен правоъгълен с катети 7 cm
4. Страната на квадрата AB = 2 \times OE = 14 cm
5. Периметър P = 4 \times AB = 56 cm
6. Лице S = AB^2 = 196 cm²
Задача 2: Докажете, че правоъгълник с перпендикулярни диагонали е квадрат.

Решение:
1. Нека ABCD е правоъгълник с AC \perp BD
2. В правоъгълника диагоналите са равни и се разполовяват, следователно AO = BO = CO = DO
3. Триъгълниците AOB, BOC, COD, DOA са равнобедрени и правоъгълни
4. От равенството на триъгълниците следва, че AB = BC = CD = DA
5. Следователно ABCD е квадрат
Задача 3: Точка M е произволна точка от страната BC на квадрата ABCD. Ъглополовящата на \sphericalangle MAD пресича страната DC в точка P. Докажете, че AM = DP + MB.

Решение:
1. Построяваме BK = DP
2. Доказваме, че \triangle APD \cong \triangle AKB (по I признак)
3. От съответните ъгли намираме, че \triangle AKM е равнобедрен
4. Следователно AM = MK = MB + BK = MB + DP
Задачи за самостоятелна работа
1. Точките E и F от диагонала на квадрата ABCD са такива, че AE = CF = AB. Докажете, че BEDF е ромб и намерете градусната мярка на ъглите му.
2. Даден е квадрат ABCD. Точка E е от страната AB. Перпендикулярът, издигнат от върха C към EC, пресича правата AD в точка F. Ъглополовящата на \sphericalangle ECF пресича правата AB в точка M. Докажете, че MC е ъглополовяща на \sphericalangle FME.
3. Външно за квадрата ABCD са построени равностранните триъгълници ABM и BCN. Намерете ъглите на \triangle MND.
4. В квадрата ABCD е построен лъч с начало точка B, който минава през вътрешността на квадрата и образува ъгъл 65^{\circ} с BC. Ако точка Q е петата на перпендикуляра, спуснат от точка D към построения лъч, намерете големината на \sphericalangle DCQ.
5. В квадрата ABCD е вписан равностранният \triangle APQ, като върховете му P и Q лежат съответно върху страните BC и DC. Ако точка F е средата на AQ и DF=2 cm, намерете периметъра на \triangle APQ.
6. Точките E и F са от диагонала AC на квадрата ABCD и AE=CF. Докажете, че BFDE е ромб.
7. Точките M, N, P и Q са съответно върху страните AB, BC, CD и AD на квадрата ABCD. Докажете, че MP\perp NQ тогава и само тогава, когато AM+CP=BN+DQ.
8. Точките E и F са от диагонала AC на квадрата ABCD и са такива, че AE=CF=AB. Докажете, че BEDF е ромб и намерете градусните мерки на ъглите му.
9. Нека ABCD е квадрат и точките M, N, P и Q са съответно от страните ме AB, BC, CD и AD така, че MP\perp NQ. Докажете, че MP=NQ.
10. През върха A на квадрата ABCD е построена произволна права, която пресича страната BC в нейна вътрешна точка M. Ъглополовящата на \sphericalangle MAD пресича страната DC в точката P. Докажете, че AP=DP+MB.
11. Даден е квадратът ABCD. Точката E е от страната AB. Перпендикулярът, издигнат от върха C към EC, пресича правата AD в точка F. Ъглополовящата на \sphericalangle ECF пресича правата AB в точка M. Докажете, че MC е ъглополовяща на \sphericalangle FME.
Видео уроци
Още обяснени и решени задачи свързани с квадрата можете да намерите в клипа ми:
Използвана литература:
1. Сборник за 7 клас, Пенка Рангелова, Константин Бекриев, Лилия Дилкина, Нина Иванова изд. Коала Прес, Пловдив, 2020
2. Тест Математика 7 клас, Донка Гълъбова, Адриана Хаджийска, Анна Аначкова и др., изд. Веди, София, 2020
3. Сборник задачи по математика за 7 клас, Мария Лилкова, Пенка Нинова, Таня Стоева и др., изд. Просвета, София
4. Книга за ученика за 7 клас, Здравка Паскалева, Мая Алашка, Райна Алашка, изд. Архимед, София, 2018
5. Текуща подготовка по математика за националното външно оценяване в 7 клас, Боянка Савова, Мария Тодорова, Веселин Златилов, изд. Просвета, София, 2020
6. Нови пробни изпити за външно оценяване и кандидатстване след 7 клас, изд. Регалия 6, София 2015
7. Тестове по математика, Любомир Любенов, Цеца Байчева, изд. DOMINO, 2017
8. Нови тематични и общи тестове по математика за 7 клас, Марина Рангелова, изд. Коала Прес, 2008
9. Учебно помагало за задължително избираема подготовка по математика за 7 клас, Иван Тонов, Таня Тонова, изд. Просвета, София, 2011
10. Тестове по математика за 7 клас, Лилия Дилкина, Константин Бекриев, изд. Коала Прес, Пловдив, 2014
11. Сборник контролни работи и тестове по математика 7 клас, Пенка Рангелова, изд. Коала Прес, Пловдив, 2009
12. Сп. Математика
13. Сп. Математика +



Коментари
Публикуване на коментар