Вписан ъгъл и периферен ъгъл 8 клас

Определение 1 Ъгъл, чийто връх лежи на дадена окръжност, а раменете му пресичат тази окръжност, се нарича вписан ъгъл.

Теорема 1 Вписаният ъгъл се измерва с половината от принадлежащата му дъга.

Пример:

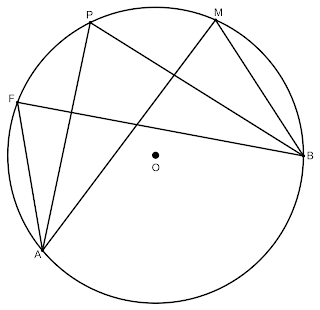
На този чертеж ъглите $\sphericalangle AFB$, $\sphericalangle APB$ и $\sphericalangle AMB$ са вписани ъгли и според Теорема 1 те са равни на половината от дъгата $\overset{\frown}{AB}$, т.е. $\sphericalangle AFB=\sphericalangle APB=\sphericalangle AMB=\frac{\overset{\frown}{AB}}{2}$.

Определение 2 Ъгъл, чийто връх лежи на дадена окръжност, едното му рамо пресича тази окръжност, а другото е допирателна към нея, се нарича периферен ъгъл.

Теорема 2 Периферният ъгъл се измерва с половината от принадлежащата му дъга.

Пример:

На този чертеж ъгъл $\sphericalangle NPQ$ е периферен ъгъл си според Теорема 2 от този урок $\sphericalangle NPQ=\frac{\overset{\frown}{AB}}{2}$.

1 Задача Отсечките $PQ$ и $QM$ са съответно диаметър и хорда в окръжността $K(O)$. Ако $\sphericalangle PQM=30^{\circ}$, намерете градусните мерки на:
а) $\sphericalangle QPM$ и $\sphericalangle POM$;

б) $\overset{\frown}{MQ}$ и $\overset{\frown}{MPQ}$.

Решение: а)

Тъй като $\sphericalangle PMQ$ е вписан ъгъл следва, че $\sphericalangle PMQ=\frac{\overset{\frown}{PQ}}{2}$. По условие обаче $PQ$ е диаметър и в такъв случай $\overset{\frown}{PQ}=180^{\circ}$, от където $\sphericalangle PMQ=90^{\circ}$. В условието ни е дадено, че $\sphericalangle PQM=30^{\circ}$ и от теоремата за сбор на ъгли в триъгълник получаваме, че $\sphericalangle QPM=60^{\circ}$. За намирането на $\sphericalangle MOP$ е достатъчно да забележим, че $\sphericalangle PQM=30^{\circ}$ е вписан ъгъл и в такъв случай принадлежащата му дъга $\overset{\frown}{MP}=60^{\circ}$, която от своя страна е равна на централния ъгъл $\sphericalangle POM$ т.е. $\overset{\frown}{MP}=\sphericalangle POM=60^{\circ}$.

б) Дъгата $\overset{\frown}{MQ}=2.\sphericalangle MPQ=120^{\circ}$ (\sphericalangle MPQ е вписан ъгъл и е равен на половината от принадлежащата му дъга). За дъгата $\overset{\frown}{MPQ}$ имаме, че $\overset{\frown}{MPQ}=\overset{\frown}{MP}+\overset{\frown}{PQ}$. Ясно е, че от факта, че $PQ$ е диаметър следва, че $\overset{\frown}{PQ}=180^{\circ}$. Сега остава да съобразим само, че $\overset{\frown}{MP}=2.\sphericalangle PQM=60^{\circ}$ (може също така да кажем, че $\overset{\frown}{MPQ}=360^{\circ}-\overset{\frown}{MQ}=240^{\circ}$) от където $\overset{\frown}{MPQ}=180^{\circ}+60^{\circ}=240^{\circ}$.

2 Задача В дадена окръжност са построени перпендикулярни хорди $MN$ и $PQ$. Намерете $\sphericalangle PQM+\sphericalangle NPQ$.

Решение:

Нека $S$ е пресечната точка на хоридте $QP$ и $MN$. Тъй като по условие $MN\perp PQ$ следва, че триъгълниците $NPS$ и $QSM$ са правоъгълни. Нека $\sphericalangle MNP=\alpha$ и $\sphericalangle NPQ=\beta$. Тъй като $\sphericalangle MNP=\sphericalangle MQP=\alpha$ (двата ъгъла са вписани и са равни на половината от дъгата $\overset{\frown}{MP}$) и $\sphericalangle QPN=\sphericalangle QMN=\beta$ (двата ъгъла са вписани и са равни на половината от дъгата $\overset{\frown}{QN}$) то следва, че  $\sphericalangle PQM+\sphericalangle NPQ=\alpha+\beta$. Но от правоъгълните триъгълници $NPS$ и $QSM$ знаем, че $\alpha+\beta=90^{\circ}$, то за търсеният сбор намираме, че $\sphericalangle PQM+\sphericalangle NPQ=90^{\circ}$.

3 Задача През точка $M$ от окръжност с център $O$ е построен диаметър $MN$ и хорда $MK$. Ако $\sphericalangle MOK-\sphericalangle NOK=68^{\circ}$, намерете ъглите на $\triangle MNK$.

Решение:

Ясно е че $\sphericalangle MOK$ и $\sphericalangle NOK$ са съседни ъгли и техният сбор е равен на $180^{\circ}$. От условието имаме, че $\sphericalangle MOK=68^{\circ}+\sphericalangle NOK$. Така получаваме, че $68^{\circ}+\sphericalangle NOK+\sphericalangle NOK=180^{\circ}$, от където намираме, че $sphericalangle NOK=54^{\circ}$, а $\sphericalangle MOK=124^{\circ}$. И двата ъгъла са централни и са равни на принадлежащите им дъги. Следователно $\overset{\frown}{MK}=124^{\circ}$ и $\overset{\frown}{KN}=56^{\circ}$. Тъй като $\sphericalangle KMN$ и $\sphericalangle MNK$ са вписани, то те са равни на половината от дъгите $\overset{\frown}{KN}$ и $\overset{\frown}{MK}$ и следователно $\sphericalangle KMN=28^{\circ}$, а $\sphericalangle KMN=62^{\circ}$. За $\sphericalangle MKN$ можем да кажем, че той е вписан ъгъл и тъй като е равен на половината от дъгата $\overset{\frown}{MN}$ следва, че  $\sphericalangle MKN=90^{\circ}$ (тай като $MN$ е диаметър по условие следва, че $\overset{\frown}{MK}=180^{\circ}$).

4 Задача Точките $A$, $B$ и $C$ лежат на окръжност с център $O$. Ако $\sphericalangle ACB=30^{\circ}$ и $AB=5 \ cm$, намерете дължината на окръжността.

Решение:

Тъй като вписаният ъгъл $\sphericalangle ACB$ е равен на $30^{\circ}$ следва, че дъгата $\overset{\frown}{AB}=60^{\circ}$, а от там и централният ъгъл $\sphericalangle AOB=60^{\circ}$. От казаното до тук можем да заключим, че триъгълникът $\triangle AOB$ е равностранен и $AO=OB=AB=5 \ cm$. Формулата за дължина на окръжност е $C=2\pi r$, където $r$ е радиусът на окръжността. Тогава за дължината на дадената окръжност имаме, че $C= 10\pi$.

5 Задача Като използвате данните от чертежа намерете $\sphericalangle ACB$ и $\sphericalangle AOB$.

Решение: Ъгъл $\sphericalangle ACB$ е вписан и той е равен на половината от дъгата $\overset{\frown}{AB}$. От дурга страна пък ъгъл $\sphericalangle AOB$ е централен и той е равен на дъгата $\overset{\frown}{AB}$. Следователно между двата ъгъла съществува равенството $2\sphericalangle ACB=\sphericalangle AOB$. От тук получаваме, че $2(x-20^{\circ})=x+55^{\circ}$. След като решим това уравнение намираме, че $x=95^{\circ}$. Тогава за търсените ъгли получаваме, че $\sphericalangle ACB=75^{\circ}$ и $\sphericalangle AOB=150^{\circ}$.

Задачи за самостоятелна работа:

1. Върху окръжност $k$ с център $O$ и диаметър $AB$ са взети точки $D$ и $C$ така, че $\overset{\frown}{AD}:\overset{\frown}{DC}:\overset{\frown}{CB}=2:3:4$. Намерете ъглите на четириъгълника $ABCD$.

2. Върховете на $\triangle ABC$ ($CA=CB$) лежат на окръжност $k$. Ъглополовящата $BL$ пресича $k$ в точката $E$ и $\sphericalangle LCE=32^{\circ}$. Намерете големината на $\sphericalangle ACB$.

3. В окръжност хордите $AB$ и $CD$ се пресичат в точка $M$ и $\sphericalangle AMD=3\sphericalangle BMD$. Намерете сбора на $\sphericalangle ACD$ и $\sphericalangle BDC$.

4.  В краищата на хорда $AB$ на дадена окръжност са построени допирателните към тази окръжност, които се пресичат в точка $T$. Да се намери $\sphericalangle ATB$, ако хордата разделя окръжността на две дъги, чиито градусни мерки се отнасят както $7:11$.

5. Хордата $AB$ в окръжност $k$ я дели на две дъги, които се отнасят както $1:4$. През точка $A$ е построена допирателна към $k$. Намерете ъглите, които хордата сключва с допирателната.

6. Диагоналът $BD$ на успоредника $ABCD$ е перпендикулярен на $BC$. Окръжност $k$ с диаметър $AD$ пресича диагонала $AC$ в точка $K$. Намерете мярката на $\sphericalangle KDB$, ако $\sphericalangle ACB=50^{\circ}$.

Още решени и обяснени задачи може да намерите във видеото ми по-долу: