Триъгълник. Сбор на ъгли в триъгълник. Външен ъгъл на триъгълник 7 клас

В настоящият урок ще научим на колко е равен сборът от ъглите в произволен триъгълник, какво е външен ъгъл на триъгълник, на колко е равен сборът от външните ъгли в триъгълника, както и ще решим някои задачи.

Теорема 1: Сборът от ъглите на всеки триъгълник е равен на ${180}^{\circ }$ или $\alpha +\beta +\gamma ={180}^{\circ }$.

Като следствие от тази теорема, можем да кажем, че всеки триъгълник има най-много един тъп ъгъл, както и, че сборът от острите ъгли в правоъгълен триъгълник е равен на ${90}^{\circ }$.

Определение 1: Външен ъгъл на триъгълник се нарича ъгъл, съседен на вътрешен ъгъл на триъгълник (в случая на чертежа външните ъгли са съответно ${\alpha }^{\prime },{\beta }^{\prime },{\gamma }^{\prime }$).

Теорема 2: Всеки вънжен ъгъл на триъгълник е равен на сбора от двата несъседни на него вътрешни ъгли на триъгълник.

Доказателство: За да унагледим доказателството ще използваме горният чертеж и разбира се Теорема 1. Тъй като $\alpha +\beta +\gamma ={180}^{\circ }$ имаме, че $\alpha ={180}^{\circ }-\beta -\gamma ={180}^{\circ }-(\beta +\gamma )$. От друга страна $\alpha$ и ${\alpha }^{\prime }$ са съседни ъгли и следователно $\alpha +{\alpha }^{\prime }={180}^{\circ }$. Сега, нека в последното равенство заменим $\alpha$ с равното му ${180}^{\circ }-(\beta +\gamma )$ и получаваме ${180}^{\circ }-(\beta +\gamma )+{\alpha }^{\prime }={180}^{\circ }$, от където ${\alpha }^{\prime }=\beta +\gamma$. Доказателството на останалите две равенства е абсолютно аналогично.

Като следствие от Теорема 2 можем да кажем, че всеки вънжен ъгъл на триъгълник е по-голям от всеки вътрешен, несъседен нему ъгъл на триъгълника.

Решени задачи

1 Задача: Намерете ъглите $\alpha$, $\beta$ и $\gamma$ на $\mathrm{△}ABC$, ако $\alpha :\beta :\gamma =2:5:3$.

Решение: Нека $\alpha =2x$, $\beta =5x$ и $\gamma =3x$, тогава от Теорема 1 имаме, че $2x+5x+3x={180}^{\circ }$ и следователно $x={18}^{\circ }$. Сега вече можем да намерим ъглите $\alpha =2\cdot {18}^{\circ }={36}^{\circ }$, $\beta =5\cdot {18}^{\circ }={90}^{\circ }$ и $\gamma =3\cdot {18}^{\circ }={54}^{\circ }$.

2 Задача: Докажете, че сборът от външните ъгли на всеки триъгълник е равен на ${360}^{\circ }$.

Решение: Нека разгледаме сборът ${\alpha }^{\prime }+{\beta }^{\prime }+{\gamma }^{\prime }$. От Теорема 2 имаме, че ${\alpha }^{\prime }=\beta +\gamma$, ${\beta }^{\prime }=\alpha +\gamma$ и ${\gamma }^{\prime }=\alpha +\beta$. Нека сега в сборът ${\alpha }^{\prime }+{\beta }^{\prime }+{\gamma }^{\prime }$ заменим всяко едно от събираемите съответно с техните равни т.е ${\alpha }^{\prime }$ с $\beta +\gamma$, ${\beta }^{\prime }$ с $\alpha +\gamma$ и ${\gamma }^{\prime }$ с $\alpha +\beta$. Така получаваме равенството ${\alpha }^{\prime }+{\beta }^{\prime }+{\gamma }^{\prime }=\beta +\gamma +\alpha +\gamma +\alpha +\beta$, от където ${\alpha }^{\prime }+{\beta }^{\prime }+{\gamma }^{\prime }=2(\alpha +\beta +\gamma )$ и тъй като $\alpha +\beta +\gamma ={180}^{\circ }$ следва, че ${\alpha }^{\prime }+{\beta }^{\prime }+{\gamma }^{\prime }={360}^{\circ }$ и задачата е решена.

3 Задача: Ъглополовящите $A{A}_1$ и $B{B}_1$ на $\mathrm{△}ABC$ се пресичат в точката $O$. Намерете $\gamma$, ако $\sphericalangle AOB={125}^{\circ }$.

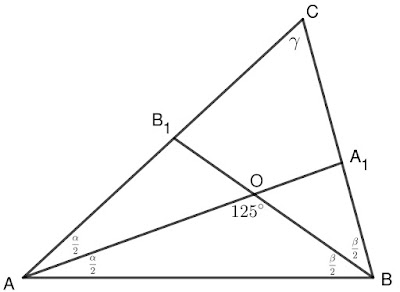
Решение: Ще използваме стандартните означения за ъглите в $\mathrm{△}ABC$. Тъй като $A{A}_1$ и $B{B}_1$ са ъглополовящи следва, че $\sphericalangle CA{A}_1=\sphericalangle A_{1}AB=\frac{\alpha }{2}$ и $\sphericalangle CB{B}_1=\sphericalangle B_{1}BA=\frac{\beta }{2}$. Според Теорема 1 за триъгълника $AOB$ имаме, че $\frac{\alpha }{2}+\frac{\beta }{2}+\sphericalangle AOB={180}^{\circ }$, следователно $\frac{\alpha }{2}+\frac{\beta }{2}+{125}^{\circ }={180}^{\circ }$, от където намираме, че $\frac{\alpha }{2}+\frac{\beta }{2}={55}^{\circ }$. Нека запишем $\frac{\alpha }{2}+\frac{\beta }{2}={55}^{\circ }$ във вида $\frac{\alpha +\beta }{2}={55}^{\circ }$. Така получаваме, че $\alpha +\beta ={110}^{\circ }$. Сега прилагаме Теорема 1 за $\mathrm{△}ABC$ и имаме, че $\alpha +\beta +\gamma ={180}^{\circ }$. Ние вече получихме, че $\alpha +\beta ={110}^{\circ }$ и следователно ${110}^{\circ }+\gamma ={180}^{\circ }$ и $\gamma ={70}^{\circ }$ с което задачата е решена.

Задачи за самостоятелна работа

1. Намерете мерките на ъглите в един триъгълник, ако те се отнасят както числата $4:3:2$.

2. Даден е $\mathrm{△}ABC$ с $\sphericalangle CAB={65}^{\circ }$ и $\sphericalangle ABC={73}^{\circ }$. Ъглополовящата $CD$ на $\sphericalangle BCA$ $(D\in AB)$ разделя дадения триъгълник на други два триъгълника - $\mathrm{△}ADC$ и $\mathrm{△}BDC$. Намерете ъглите на тези триъгълници.

3. Ако мерките на външните ъгли на триъгълник се отнасят както $4:3:5$, намерете вътрешните му ъгли.

4. В триъгълник един от вътрешните му ъгли е ${40}^{\circ }$, а един външен ъгъл е ${30}^{\circ }$. Намерете ъглите на този триъгълник.

5. В триъгълника $ABC$ е известно, че $\sphericalangle A$ е с 10% по-голям от $\sphericalangle B$ и тъпият ъгъл между ъглополовящите $AL$ и $CN$ е равен на ${115}^{\circ }$. Да се намери $\sphericalangle C$.

Видео уроци:

Още обяснени и решени задачи свързани с този урок можете да намерите в клипа ми даден по-долу:

Използвана литература:

1. Сборник за 7 клас, Пенка Рангелова, Константин Бекриев, Лилия Дилкина, Нина Иванова изд. Коала Прес, Пловдив, 2020

2. Тест Математика 7 клас, Донка Гълъбова, Адриана Хаджийска, Анна Аначкова и др., изд. Веди, София, 2020

3. Сборник задачи по математика за 7 клас, Мария Лилкова, Пенка Нинова, Таня Стоева и др., изд. Просвета, София

4. Книга за ученика за 7 клас, Здравка Паскалева, Мая Алашка, Райна Алашка, изд. Архимед, София, 2018

5. Текуща подготовка по математика за националното външно оценяване в 7 клас, Боянка Савова, Мария Тодорова, Веселин Златилов, изд. Просвета, София, 2020

6. Нови пробни изпити за външно оценяване и кандидатстване след 7 клас, изд. Регалия 6, София 2015

7. Тестове по математика, Любомир Любенов, Цеца Байчева, изд. DOMINO, 2017

8. Нови тематични и общи тестове по математика за 7 клас, Марина Рангелова, изд. Коала Прес, 2008

9. Учебно помагало за задължително избираема подготовка по математика за 7 клас, Иван Тонов, Таня Тонова, изд. Просвета, София, 2011

10. Тестове по математика за 7 клас, Лилия Дилкина, Константин Бекриев, изд. Коала Прес, Пловдив, 2014

11. Сборник контролни работи и тестове по математика 7 клас, Пенка Рангелова, изд. Коала Прес, Пловдив, 2009

12. Сп. Математика

13. Сп. Математика +