Множества. Основни понятия - обединение, сечение, разлика и допълнение на множества

Основоположник на теорията на множествата е Георг Кантор (1845-1918) (повече за историята на теорията на множествата виж тук). Понятието множество е фундаментално и не се определя чрез други понятия, а се описва и обеснява интуитивно. Най-общо казано, за множество можем да считаме всяка съвкупност от определени и различни един от друг обекти, които човек може да измисли и да приеме, като едно цяло. Множество например е нашата азбука, която се състои от $30$ букви; учениците в класната стая; молекулите съставящи човешкото тяло; звездите в Млечният път и т.н.

Ще считаме, че едно множество е добре дефинирано, ако са определени неговите обекти, от които то е съставено. Допустими обекти са протоелементите и самите множества.  Тези елементи трябва да са различни един от друг и за всеки елемент е необходимо да се знае дали той принадлежи или не принадлежи към дадено множество, както и дали всеки два обекта на множеството са различни или съвпадат. При образуване на едно множество, за негови елементи могат да се посочват протоелементи, или вече образувани от предходни стъпки множества. Така, ако вече сме образували едно множество, то може да е елемент на друго множество. 

Определение 1: Множество от множества ще наричаме фамилия от множества.

Множествата обикновено ще бележим с големи латински букви $A$, $B$, $C$ и т.н. а елементите с малки латински букви $a$, $b$, $c$,$\ldots$, $x$, $y$, $z$ и т.н. В някои източници могат да се използват и малки букви от гръцката азбука $\alpha$, $\beta$, $\gamma$ и т.н. 

Определение 2: Твърдението, че "елементът $x$ принадлежи на множеството A" ще бележим по следният начин $x\in A$ (четем "$x$ принадлежи на $A$"). Ако емелентът $x$ не принадлежи на множеството $A$, ще бележим с $x\notin A$ (четем "$x$ не принадлежи на $A$").

От това определение следва, че ако множеството $A$ е дефинирано то за всеки елемент $x$ е вярно едно от двете твърдения "$x$ принадлежи на $A$" или "$x$ не принадлежи на $A$". Например ако разгледаме множеството $A=\{1,2,3,4,5\}$ за него е вярно, че $1\in A$, $4\in A$, $5\in A$, но $0\notin A$, $10\notin A$ и т.н.

Множествата могат да бъдат зададени чрез изброяване на елементите им или чрез посочване на някакво тяхно свойство.Множеството $A$, което се състои от всички елементи $x$, които притежават свойството $f(x)$ ще записваме по следният начин: $A=\{x:f(x)\}$. Често се използва и записът $A=\{x|f(x)\}$. Като пример на казаното можем да запишем "Множеството $B$, което се състои от корените на уравнението $x^2-5x+6=0$", като $B=\{x:x^2-5x+6=0\}$, от където лесно се вижда, че $B=\{3, 2\}$.

На читателя вероятно вече са добре познати числовите множества:

$\mathbb{N}=\{1,2,3,4,5\ldots\}$ - множеството на естествените числа;

$\mathbb{Z}=\{\ldots,-2,-1,0,1,2,\ldots\}$ - множеството на целите числа;

$\mathbb{Q}=\{\frac{p}{q}:p\in\mathbb{Z}, q\in\mathbb{Z},q\neq 0\}$ - множеството на рационалните числа;

$\mathbb{I}$ - множество на ирационалните числа;

$\mathbb{R}$ - множество на реалните числа;

$\mathbb{C}$ - множество на комплексните числа.

Определение 3: Броят на елементите на множеството $A$ ще означаваме с $|A|$ и ще наричаме мощност на множеството $A$.

Например, ако разгледаме множеството $B=\{2,4,6,8,10\}$, то $|B|=5.$

Определение 4: Множеството което не съдържа нито един елемент ще наричаме празното множество и ще означаваме с $\emptyset$.

Аксиома за обема: Ако за всяко $x$ е изпълнено, че $x\in A\iff x\in B$, то следва, че $A=B.$

Аксиома за отделянето: Нека $A=\{x:x\in A, f(x)\}$ е множество и да въведем понятието предикат $P(x)$, където $x\in M$ е параметризизиран въпрос с два възможни отговора (истина и лъжа) и този отговор зависи от параметъра $x$. Тогава, ако $B=\{x:P(x)=истина, x\in A\}$, то $B$ е множество и $B$ се нарича подмножество на $A$ (ще казваме още, че $A$ съдържа $B$) и записваме $B\subseteq A$ ($A\supseteq B$), ако $A\neq B$ пишем $B\subset A$ ($A\supset B$).

$B\subset A$

Аксиома за степента: Съвкупността от всички подмножества на множеството $A$ е множество.

С множествата можем да извършваме различни операции.

Определение 5: Обединението на множеството $A$ с множеството $B$ се състои от всички елементи, които принадлежат поне на едно от двете множества. Обединението означаваме по следният начин $A\cup B=\{x:x\in A\ или\ x\in B\}.$

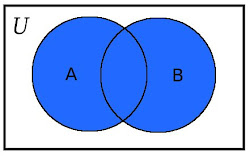$A\cup B$

Например, ако разгледаме множествата $A=\{1,2,3,4,5\}$ и $B=\{3,4,5,6,7,8,9\}$, тогава $A\cup B=\{1,2,3,4,5,6,7,8,9\}$.

Определение 6: Сечението на множеството $A$ с множеството $B$ се състои от всички елементи, които принадлежат на множеството $A$ и на множеството $B$ (всички елементи които принадлежат едновременно и на двете множества). Сечението означаваме по следният начин $A\cap B=\{x:x\in A\ и\ x\in B\}.$

$A\cap B$

Например, ако разгледаме множествата $A=\{a,b,c,d,e\}$ и $B=\{c,d,e,f,g\}$, тогава $A\cap B=\{c,d,e\}$.

Определение 7: Разликата $A\setminus B$ на множествата $A$ и $B$ се състои от всички елементи, които принадлежат на множеството $A$, но не принадлежат на множеството $B$, т.е. $A\setminus B=\{x:x\in A\ и \ x\notin B\}$

$A\setminus B$

Например, ако разгледаме множествата $A=\{a,b,c,d,e\}$ и $B=\{c,d,e\}$, тогава $A\setminus B=\{a,b\}$.

Като следствие от Определение 7 имаме, че ако $A\subseteq B$, тогава $A\setminus B=\emptyset$ и, ако $A\cap B=\emptyset$, тогава $A\setminus B=A.$

Определение 8: Симетрична разлика на множествата $A$ и $B$ ще наричаме множеството $A\triangle B=(A\setminus B)\cup(B\setminus A).$

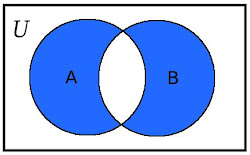$A\triangle B$

Определение 9: Универсално множество (универсум) ще наричаме множеството на което всички множества са подмножества и ще го отбелязваме с $U$.

Определение 10: Полученото множество от разликата $U\setminus A$ се нарича допълнение на $A$ до $U$ и се бележи с $\overline A.$ 

Свойства на основните операции с множества:

1. Идемпотентност:

$A\cup A=A$ и $A\cap A=A$.

2. Комутативност:

$A\cup B=B\cup A$; $A\cap B=B\cap A$ и $A\triangle B=B\triangle A$.

3. Асоциативност:

$(A\cup B)\cup C=A\cup(B\cup C)$; $(A\cap B)\cap C=A\triangle (B\triangle C)$ и $(A\triangle B)\triangle C=A\triangle (B\triangle C).$

4. Дистрибутивност:

$(A\cup B)\cap C=(A\cap C)\cup (B\cap C)$ и $(A\cap B)\cup C=(A\cup C)\cap (B\cup C)$.

Закони на Де Морган: За произволни множества $A$ и $B$ са изпълнени равенствата $\overline{A\cup B}=\overline A\cap\overline B$ и $\overline{A\cap B}=\overline A\cup\overline B.$ 

1 Задача Дадено е множеството $A=\{21,\frac{11}{3},\frac{3}{12},\sqrt{28},-1\}$, да се намери мощността на множеството $A$.

Решение: От Определение 3 знаем, че за да намерим мощността на едно множество е необходимо да знаем броя на неговите елементи. Очевидно за даденото множество, можем да кажем, че $|A|=5.$

2 Задача Дадени са множествата $A=\{2,3,4,8\}$, $B=\{1,3,4,8\}$ и $C=\{2,4,8,9\}$. Да се намери множеството $(A\cap C)\cup (B\cap C).$

Решение: Формираме множествата $(A\cap C)=\{2,4,8\}$ и $(B\cap C)=\{4,8\}$, следователно $(A\cap C)\cup (B\cap C)=\{2,4,8\}.$

3 Задача Да се докаже, че $(A\cup B)\cap C=(A\cap C)\cup (B\cap C).$

Решение: Нека $M=(A\cup B)\cap C$ и $N=(A\cap C)\cup (B\cap C).$ За да докажем равенството трябва да покажем, че $M\subseteq N$ и $N\subseteq M.$ 

I. Ще докажем, че $M\subseteq N$ т.е. $(A\cup B)\cap C\subseteq (A\cap C)\cup (B\cap C).$

Ако $M=\emptyset$, тогава имаме, че $\emptyset\subseteq N$, което е вярно за всяко множество $N$. Да предположим, че $M\neq\emptyset$. Избираме произволен елемент $x\in M$, следователно $x\in (A\cup B)$ и $x\in C$. Разглеждаме следните три случая:

1 сл. $x\in A$, $x\in B$ и $x\in C$, следователно $x\in (A\cap C)$ и $x\in (B\cap C)$, от където имаме, че $x\in N$.

2 сл. $x\in A$, $x\notin B$ и $x\in C$, следователно $x\in (A\cap C)$ и $x\notin (B\cap C)$, от където имаме, че $x\in N$.

3 сл. $x\notin A$, $x\in B$ и $x\in C$, следоватевно $x\notin (A\cap C)$ и $x\in (B\cap C)$, от където имаме, че $x\in N$.

Така и в трите случая получихме, че $x\in N$, следователно $M\subseteq N.$

II. Ще докажем, че $N\subseteq M$ т.е. $(A\cap C)\cup (B\cap C)\subseteq (A\cup B)\cap C.$

Ако $N=\emptyset$, тогава имаме, че $\emptyset\subseteq M$, което е вярно за всяко множество $M$. Да предположим, че $N\neq\emptyset.$ Избираме произволен елемент $x\in N$, и получаваме следните три случая:

1 сл. $x\in (A\cap C)$ и $x\in (B\cap C)$, следователно $x\in A$, $x\in B$ и $x\in C$, от където $x\in (A\cup B)$ и $x\in C$, така получаваме, че $x\in M$.

2 сл. $x\in (A\cap C)$ и $x\notin (B\cap C)$, следователно $x\in A$, $x\in C$ и $x\notin B$, от където $x\in (A\cup B)$ и $x\in C$, така получаваме, че $x\in M$.

3 сл. $x\notin (A\cap C)$ и $x\in (B\cap C)$, следователно $x\notin A$, $x\in B$ и $x\in C$, от където $x\in (A\cup B)$ и $x\in C$, така получаваме, че $x\in M$.

Така и в тези три случая получихме, че $x\in M$, следователно $N\subseteq M$, с което и доказателството на равенството е окончателно доказано.

4 Задача Да се докаже, че $(A\cap B)\setminus C=(A\setminus C)\cap (B\setminus C).$

Решение: Нека $M=(A\cap B)\setminus C$ и $N=(A\setminus C)\cap (B\setminus C).$ За да докажем равенството трябва да покажем, че $M\subseteq N$ и $N\subseteq M$.

I. Ще докажем, че $M\subseteq N$ т.е. $(A\cap B)\setminus C\subseteq (A\setminus C)\cap (B\setminus C)$. 

Ако $M=\emptyset$, тогава имме, че $\emptyset\subseteq N$, което е вярно за всяко множество $N$. Да предположим, че $M\neq\emptyset$.

Избираме произволен елемент $x\in M$, следователно $x\in (A\cap B)$ и $x\notin C$, т.е. $x\in A$, $x\in B$ и $x\notin C$, от където следва, че $x\in (A\setminus C)$ и $x\in (B\setminus C)$ и така получаваме, че $x\in N$.

II. Ще докажем, че $N\subseteq M$ т.е. $(A\setminus C)\cap (B\setminus)\subseteq (A\cap B)\setminus C$. 

Ако $N=\emptyset$, тогава имаме, че $\emptyset\subseteq M$, което е вярно за всяко множество $M$. Да предположим, че $N\neq\emptyset$.

Избираме произволен елемент $x\in N$, следователно $x\in (A\setminus C)$ и $x\in (B\setminus C)$, от където имаме, че $x\in A$, $x\in B$ и $x\notin C$, следователно $x\in (A\cap B)$ и $x\notin C$, така получаваме, че $x\in M$ и $N\subseteq M$, с което равенството е доказано. 

Задачи за самостоятелно работа

1. Дадени са множествата $A=\{2,3,4,5,6\}$, $B=\{1,3,6,12\}$ и $C=\{1,4,6,15\}$. Намерете множеството $(A\cup B)\cap (B\cup C).$

2. Да се докаже, че $(A\cap B)\cup C=(A\cup C)\cap (B\cup C).$

3. Да се докаже, че $A\setminus(B\cup C)=(A\setminus B)\cap (A\setminus C).$

4. Проверете вярно ли е равенството $(A\cap B)\setminus (A\setminus C)=A\cap B\cap C.$

5. Докажете, че $A\setminus (A\cap B)=A\setminus B$.

6. Ако $A=\{1,2\}$, $B=\{1,2,4,5\}$ и $C=\{5,7,9,10\}$ намерете:

а) $A\cup B$; б) $A\cap B$; в) $(A\cup B)\cup C$; г) $(A\cap B)\cap C$; д) $(A\cup B)\cap C$; е) $(A\cap B)\cup C$.

7. Ако $U=\{1,2,3,4,\ldots, 10\}$, $A=\{x\in U: x \ е \ просто \ число\}$, $B=\{x\in U: x \ е \ нечетно\}$ покажете, че $A\cap B=A\cup B$.

8. $U=\{a, b, c, d, e, f, g\}$, $A=\{a, b, c, d\}$, $B=\{a, b, c ,d, e, f\}$ и $C=\{a, b, g\}$ намерете $\overline{A}$, $\overline{B}$, $\overline{C}$, $A\setminus B$, $B\setminus C$, $A\cap B$, $A\cup B$ и $B\cap C$. 

9. Ако $U=\{x\in\mathbb{Z}:-5<x<5\}$ и $A=\{x\in\mathbb{Z}:-2<x<3\}$ опишете елементите на множествата $\overline{A}$, $\overline{A}\cap\overline{A}$, $A\cap U$ и $A\cup U$.

10. Ако $A$ и $B$  са две дадени множества докажете, че $A\cap (B\setminus A)=\emptyset$.

11. Ако $A=\{1,2,3,4\}$, $B=\{2,3,4,5\}$ и $C=\{1,3,4,5,6,7\}$ проверете вярно ли е равенството $A\cap (B\cup C)=(A\cap B)\cup (A\cap C)$.

12. Ако $A=\{1,3,5,7,9\}$ и $B=\{3,5,8\}$, тогава намерете $A\triangle B$ (симетричната разлика на множествата $A$ и $B$)

13. Проверете равенствата:

а) $B\cup\left(\displaystyle\cup_{i=1}^{3}A_i\right)=\displaystyle\cap_{i=1}^{3}(B\cup A_i)$;

б)  $B\cup\left(\displaystyle\cap_{i=1}^{3}A_i\right)=\displaystyle\cup_{i=1}^{3}(B\cap A_i)$

14. Нека $A$, $B$ и $C$ са множества. Покажете че $\overline{A\cup(B\cap C)}=(\overline{C}\cup\overline{B})\cap\overline{A}$.

15. Нека $A=\{0,2,4,6,8\}$, $B=\{0,1,2,3,4\}$ и $C=\{0,3,6,9\}$. Намерете $A\cup B\cup C$ и $A\cap B\cap C$.

16. Да се докаже, че:

а) $\overline{\cup^{\infty}_{i=1}A_i}=\cap_{i=1}^{\infty}\overline{A_i}$; б)  $\overline{\cap^{\infty}_{i=1}A_i}=\cup_{i=1}^{\infty}\overline{A_i}$.

17. Докажете, че ако $A$, $B$ и $C$ са множества, тогава
$|A\cup B\cup C|=|A|+|B|+|C|-|A\cap B|-|A\cap C|-|B\cap C|-|A\cap B\cap C|$.

18. Нека $A$, $B$ и $C$ са множества. Покажете, че $(A\setminus B)\setminus C=(A\setminus C)\setminus (B\setminus C)$.

19. Нека $A=\{0,2,4,6,8,10\}$, $B=\{0,1,2,3,4,5,6\}$ и $C=\{4,5,6,7,8,9,10\}$. Намерете:

а) $A\cap B\cap C$; б) $A\cup B\cup C$; в) $(A\cup B)\cap C$; г) $(A\cap B)\cup C$.

20. Нека $A$, $B$ и $C$ са множества. Начертайте диаграми на Ойлер - Вен за всяко от множествата:

а) $A\cap (B\cup C)$; б) $\overline{A}\cap\overline{B}\cap\overline{C}$; в) $(A\setminus B)\cup (A\setminus C)\cup (B\setminus C)$.

21. Нека $A$, $B$ и $C$ са множества. Начертайте диаграми на Ойлер - Вен за всяко от множествата:

а) $A\cap (B\setminus C)$; б) $(A\cap B)\cup (A\cap C)$; в) $(A\cap\overline{B})\cup (A\cap\overline{C})$.

22. Нека $A$, $B$ и $C$ са множества. Начертайте диаграми на Ойлер - Вен за всяко от множествата:

а) $(A\cap B)\cup (C\cap D)$; б) $\overline{A}\cup\overline{B}\cup\overline{C}\cup\overline{D}$; в) $A\setminus(B\cap C\cap D)$.

Използвана литература:

1. Дискретна математика, Светла Бойчева, Стефка Толева-Стоименова, изд. Сиела 2018 г.

2. Увод в дискретната математика, Красимир Манев, изд. КЛМН 2012 г.

3. Въведение в дискретната математика, Христо Кискинов, Пловдивско университетско издателство