Централни ъгли, дъги и хорди. Диаметър перпендикулярен на хорда 8 клас
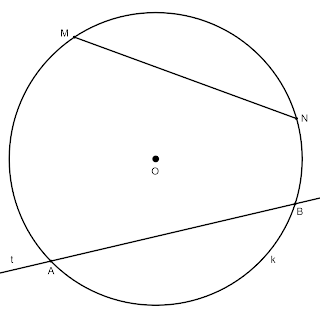
Ако права t пресича окръжността k в точка A и точка B, те определят отсечката AB, която се нарича хорда за окръжността k. Отсечката MN е също хорда за окръжността k.
Определение 1: Всяка хорда разделя окръжността на две части, които се наричат дъги на окръжността.
Ако хордата AB е диаметър на дадена окръжност, то всяка от дъгите \overset{\frown}{ALB} и \overset{\frown}{AKB} се нарича полуокръжност и \overset{\frown}{ALB}=\overset{\frown}{AKB}.
Определение 2: Ъгъл чийто връх е център на дадена окръжност k се нарича централен ъгъл.
Всеки централен ъгъл е равен на принадлежащата му дъга.
Например на даденият чертеж \sphericalangle KOL е централен ъгъл и \sphericalangle KOL=\overset{\frown}{KL}=\alpha.
Определение 2 Две окръжности се наричат еднакви ако имат равни радиуси.
Определение 3 Две дъги от една и съща окръжност или от еднакви окръжности се наричат равни, когато имат равни мерки (в градуси).
1) Ако AB=CD следва, че \alpha=\beta и \overset{\frown}{AB}=\overset{\frown}{CD}.
2) Ако \overset{\frown}{AB}=\overset{\frown}{CB} следва, че \alpha=\beta и AB=CD.
3) Ако \alpha=\beta следва, че \overset{\frown}{AB}=\overset{\frown}{CB} и AB=CD.
Ако AB\parallel CD, то \overset{\frown}{AC}=\overset{\frown}{BD} и обратно, ако \overset{\frown}{AC}=\overset{\frown}{BD}, то AB\parallel CD. Сега като приложим горната теорема следва, че хордите AC и BD са равни и ABCD е равнобедрен трапец.
Теорема 2 В окръжност диаметър перпендикулярен на хорда я разполовява
Доказателство:
Доказателството на тази теорема е елементарно. Построяваме радиусите OK и OL. Триъгълникът KLO е равнобедрен. Тъй като OH е височина в този триъгълник (диаметъра AB) е перпендикулярен на хордата KL и \sphericalangle OKL=\sphericalangle OLK=90^{\circ}), то OH е и медиана (както й ъглополовяща) от където следва, че точката H е среда на KL.
Теорема 3 Ако в окръжност диаметър минава през средата на хорда, която не е диаметър, то той е перпендикулярен на хордата.
Доказателство: За онагледяване на доказателството ще използваме чертежа от Теорема 2. Разликата тук е в това, че вместо да имаме като дадено, че AB\perp KL имаме KH=LH. И тъй като \triangle KOL е равнобедрен и точката H е среда на KL следва, че OH е медиана височина и ъглополовяща, от където следва, че OH\perp KL, т.е. AB\perp KL.
Ще кажем и още някои неща, които е добре да запомним и, които се използват при решаването на задачи.
1) В окръжност диаметър перпендикулярен на дадена хорда, разполовява съответната дъга.
2) Две хорди в една окръжност са равни, ако разстоянията от центъра на окръжността до хордите са равни.
3) Ако две хорди в една окръжност не са равни, по-голямата от тях е по-близо до центъра. Обратно, ако разстоянията от центъра на една окръжност до две нейни хорди са различни, то по-близо до центъра е по-голямата хорда.
Сега да разгледаме някои задачи.
1 Задача Точките A, B, C и D взети в този ред, са от окръжност k и \overset{\frown}{AB}:\overset{\frown}{BC}:\overset{\frown}{CD}:\overset{\frown}{DA}=6:4:2:3. Намерете градусните мерки на дъгите \overset{\frown}{ABC}, \overset{\frown}{BCD} и \overset{\frown}{DAB}.
Решение:
Нека \overset{\frown}{AB}=6x, \overset{\frown}{BC}=4x, \overset{\frown}{CD}=2x и \overset{\frown}{DA}=3x. Тъй като 6x+4x+2x+3x=360^{\circ} (нека да припомним, че цялата окръжност е 360^{\circ}), тогава получаваме, че 15x=360^{\circ}, от където x=24^{\circ}. Следователно \overset{\frown}{AB}=6x=6.24^{\circ}=144^{\circ}, \overset{\frown}{BC}=4x=4.24^{\circ}=96^{\circ}, \overset{\frown}{CD}=2x=2.24^{\circ}=48^{\circ} и \overset{\frown}{DA}=3x=3.24^{\circ}=72^{\circ}.
Тъй като дъгата \overset{\frown}{ABC}=\overset{\frown}{AB}+\overset{\frown}{BC} то за \overset{\frown}{ABC} получаваме \overset{\frown}{ABC}=144^{\circ}+96^{\circ}=240^{\circ}. За дъгата \overset{\frown}{BCD} имаме че \overset{\frown}{BCD}=\overset{\frown}{BC}+\overset{\frown}{CD} и следователно \overset{\frown}{BCD}=96^{\circ}+48^{\circ}=144^{\circ}. Накрая за дъгата \overset{\frown}{DAB} имаме, че \overset{\frown}{DAB}=\overset{\frown}{DA}+\overset{\frown}{AB} и тогава \overset{\frown}{DAB}=72^{\circ}+144^{\circ}=216^{\circ}.
2 Задача Градусната мярка на дъгата \overset{\frown}{MN} е \frac{1}{4} от тази на окръжността k(O). Ако MN=12\sqrt{5} \ dm, то намерете разстоянието от O до MN.
Решение:
Построяваме радиусите OM и ON. Тъй \overset{\frown}{MN} е \frac{1}{4} от тази на окръжността следва, че \overset{\frown}{MN}=\frac{1}{4}.360^{\circ}=90^{\circ}. От тук получаваме, че и \sphericalangle MON=90^{\circ} (той е централен ъгъл). Можем да кажем също и, че \sphericalangle ONM=\sphericalangle OMN=45^{\circ} и \triangle MON е равнобедрен и правоъгълен. Следователно OH=HM=HN и тъй като OH е височина, медиана и ъглополовяща то точката H е среда на MN. От тук следва, че OH=HM=\frac{1}{2}MN=6\sqrt{5} \ dm.
3 Задача Дадени са хорда AB=7 \ cm и дъга \overset{\frown}{AB}=60^{\circ} от окръжност k. Намерете диаметъра на k.
Решение:
Построяваме радиусите OA и OB. От това, че \overset{\frown}{AB}=60^{\circ} следва, че централният ъгъл \sphericalangle AOB=60^{\circ}. Тъй като \triangle AOB е равнобедрен триъгълник с ъгъл равен на 60^{\circ} то следва, че \triangle ABO е равностранен триъгълник и AB=OA=OB=r=7 \ cm. Диаметърът на окръжност k е равен на 2r и следователно d=2r=2.7=14 \ cm.
4 Задача В окръжност са дадени хордите AB и CD. Докажете, че ако:
а) AB=CD, разстоянията от центъра O на окръжността до хордите са равни;
б) разстоянията от центъра O на окръжността до хордите са равни, то AB=CD.
Решение: а)
Нека разстоянието от точката O до хордата AB е OH, а до хордата CD е OM. Построяваме радиусите OA, OB, OC и OD.
Не е трудно да се види, че \triangle AOB\cong\triangle COD по трети признак и следователно OH=OM (съответните височини в еднаквите триъгълници са равни).
Може също така да кажем и, че от OH\perp AB и OM\perp CD и \triangle AOB и COD - равнобедрени следва, че AH=HB=DM=MC (OH и OM са височини, медиани и ъглополовящи), от където HB=DM. Така от казаното до тук лесно се доказва, че \triangle BHO\cong\triangle DOM (правоъгълни триъгълници) по четвърти признак и OH=OM.
б) Сега имаме, че OH=OM и трябва да докажем, че AB=CD.
Тъй като \triangle HOB\cong\triangle MOD по четвърти признак следва, че HB=DM. Аналогично \triangle AHO\cong\triangle CMO и следователно AH=CM, от където и AB=CD.
Задачи за самостоятелна работа:
1. Хордата BC на окръжност с център O е равна на радиуса на окръжността. Ако AB е диаметър, намерете ъглите на \triangle ABC.
2. Върху окръжност с център O са взети точките A, B, C и D в този ред. За непресичащите се дъги \overset{\frown}{BC}, \overset{\frown}{CD} и \overset{\frown}{DA} е дадено, че \overset{\frown}{DA}=3\overset{\frown}{CD} и 5\overset{\frown}{CD}=2\overset{\frown}{BC}. Намерете \sphericalangle AOB, \sphericalangle BOC, \sphericalangle COD и \sphericalangle DOA, ако \overset{\frown}{AB}=100^{\circ}.
3.Точките M и N лежат на окръжност k(O;r=10 \ cm). Намерете мярката на \overset{\frown}{MN}, ако точка O е на разстояние 5 \ cm от хордата AB.
4. Точките M, N и P са от окръжност с център O. Ако \overset{\frown}{MN}=60^{\circ} и дъгата \overset{\frown}{NP}, несъдържаща точката M е 4 пъти по-голяма от дъгата \overset{\frown}{MN}. Намерете:
а) мярката на \sphericalangle MOP;
б) периметъра на четириъгълника MNOP, ако хордата MP е 7 \ cm.
5. Дадена е окръжност с център O и хорда MN. Докажете, че ъглополовящата на \sphericalangle MON пресича дъгата \overset{\frown}{MN} в средата й.
Още решени и обяснени задачи може да намерите във видеото ми по-долу:
.png)


.png)


.png)
.png)




Коментари
Публикуване на коментар