Линейна функция, графика на линейна функция 9 клас

Определение 1: Функция от вида $f(x)=kx+n$, където $k,n\in\mathbb{R}$, а $x$ е променлива се нарича линейна функция.

Числата $k$ и $n$ се наричат още коефициенти.

Коефициентът $k$ e така нареченият ъглов коефициент и в зависимост от стойностите му графиката на линейната функция (която е правата) сключва различни ъгли с оста $O_x$. В следващият пример ще покажем какви ъгли сключва правата с оста $O_x$ за различните стойности на $k$.

Пример 1: Разглеждаме графиката на функцията $f(x)=2x+1$.

  

Пример 2: Разглеждаме графиката на функцията $f(x)=10x+1$.

Пример 3: Разглеждаме графиката на функцията $f(x)=-2x+1$.

Пример 4: Разглеждаме графиката на функцията $f(x)=-10x+1$.

На дадените графики не е трудно да забележим, че пресечната точка на правата с оста $O_y$ е точно в единицата. Това не е случайно. Коефициентът $n$ (който в нашият случай е 1 за всяка от графиките) показва именно къде графиката на линейната функция пресича оста $O_y$.

Важно е да споменем още и някои други свойства на линейните функции. Ако имаме линейните функции $f_1(x)=k_1x+n_1$ и $f_2(x)=k_2x+n_2$, както вече видяхме графиките им са прави. Ако $k_1$ и $k_2$ са равни и $n_1\neq n_2$, то тогава двете прави ще бъдат успоредни. 

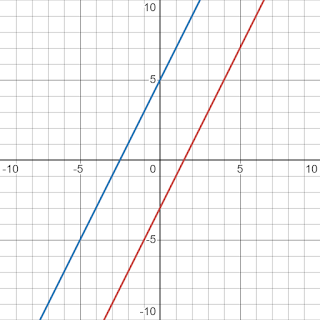
Пример 5: На долната фигура виждате графиките на функциите $f_1(x)=2x-3$ (червената) и $f_2(x)=2x+5$ (синята).

Отново можем да се уверим, че пресечните точки на двете функции с оста $O_y$ отново са съответно в $-3$ и $5$, което както отбелязахме по-горе не е случайност а зависи от коефициента $n$ на линейната функция.

Също така, графиките на две линейни функции $f_1(x)=k_1x+n_1$ и $f_2(x)=k_2x+n_2$ са перпендикулярни, ако $k_1.k_2=-1$.

Пример 6: Разглеждаме графиките на функциите $f_1(x)=\frac{1}{2}x-1$ (червената) и $f_2(x)=-2x+3$ (синята).

1 Задача Проверете кои от точките $A(-5;-4)$, $B(-3;-5)$, $C(-1,5;-4)$, $D(0;-3)$ и $E(1;\frac{2}{3})$ лежат на графиката на функцията $f(x)=\frac{2}{3}x-3$.

Решение: Ще направим първо проверка за $A(-5;-4)$. Заместваме във функцията $x=-5$, а $y=-4$, така получаваме $-4=\frac{2}{3}.(-5)-3$ (припомняме, че $y=f(x)$ т.е. $y=-4$ заместваме на мястото на $f(x)$). Сега трябва да проверим дали горното числово равенство е вярно. Ако е вярно значи точката $A$ е от графиката на функцията, ако не е вярно значи точката не е от графиката й. Пресмятаме $\frac{2}{3}.(-5)-3=-\frac{10}{3}-3=-\frac{19}{3}\neq -4$ и следователно числовото равенство е грешно, от където можем да заключим, че точката $A(-5;-4)$ не е от графиката на функцията.

Проверяваме точката $B(-3;-5)$ отново по същият начин заместваме $x$ и $y$ във функцията и имаме $-5=-\frac{2}{3}.(-3)-3$. Дясната страна на това равенство е равна на $-1$, което е различно от $-5$ и следователно точката $B(-3;-5)$ не е от графиката на функцията.

Сега правим проверка за $C(-1,5;-4)$. Заместваме във функцията и получаваме $-4=-\frac{2}{3}.(-1,5)-3$. Дясната страна на това числово равенство е равна на $-2$ и тъй като $-4\neq -2$ това означава, че точката $C(-1,5;-4)$ също не е от графиката на функцията.

Разглеждаме точката $D(0;-3)$. Заместваме във функцията и имаме $-3=-\frac{2}{3}.0-3$. Дясната страна на последното равенство е равна на $-3$, следователно лявата и дясната страна са равни и имаме вярно числово равенство, което ни показва, че точката $D(0;-3)$ е от графиката на функцията. 

Накрая остана да направим проверка за точката $E\left(1;\frac{2}{3}\right)$. Заместваме във функцията и получаваме $\frac{2}{3}=-\frac{2}{3}.1-3$. Дясната страна на това числово равенство е равна на $-\frac{11}{3}$ и $\frac{2}{3}\neq -\frac{11}{3}$, следователно точката $E\left(1;\frac{2}{3}\right)$ не е от графиката на функцията.

2 Задача Определете дали графиките на всяка двойка функции са успоредни, съвпадащи или нито едно от двете:
а) $3x-4y=12$ и $9x-12y=72$; б) $15x+12y=36$ и $5x+4y=12$.

Решение: а) Записваме всяка от функциите във вида $y=\frac{3}{4}x-3$ и $y=\frac{3}{4}x-6$. Тъй като ъгловите коефициенти на двете функции са равни, а свободните членове са различни от казаното по-горе може да заключим, че графиките на двете функции са успоредни.

б) Записваме всяка от функциите във вида $y=-\frac{5}{4}x+3$ (предварително делим лявата и дясната страна на $3$ и получаваме $5x+4y=12$) и $y=-\frac{5}{4}x+3$. В този случай ъгловите коефициенти на двете функции са равни, както и свободните им членове. Това ни показва, че графиките на двете функции съвпадат.

3 Задача Намерете функция графиката, на която минава през точката $A(4;-7)$ и е успоредна с графиката на функцията $f(x)=\frac{2}{5}x+\frac{8}{5}$.

Решение: Търсим функция от вида $f(x)=kx+n$. В условието на задачата ни е казано, че графиката на търсената функция трябва да е успоредна с графиката на функцията $f(x)=\frac{2}{5}x+\frac{8}{5}$. Следователно от тук имаме, че $k=\frac{2}{5}$ и $n\neq\frac{8}{5}$, т.е. търсената функция придобива вида $f(x)=\frac{2}{5}x+n$. Сега остава да намерим $n$. Тъй като в условието още е дадено, че графиката на търсената функция минава през точката $A(4;-7)$, като заместим $x=4$ и $y=-7$ в търсената функция получаваме, че $-7=\frac{2}{5}.4+n$. Последното равенство можем да разгледаме, като уравнение, в което неизвестното е $n$. Така решавайки го получаваме, че $n=-\frac{43}{5}$. Следователно търсената функция е $f(x)=\frac{2}{5}x-\frac{43}{5}$.

4 Задача Намерете функция графиката, на която минава през точката $A(-6;-1)$ и е перпендикулярна с графиката на функцията $f(x)=-\frac{4}{3}x+\frac{7}{3}$.

Решение: Търсим функция от вида $f(x)=kx+n$. В условието на задачата ни е казано, че графиката на търсената функция трябва да е перпендикулярна с графиката на функцията $f(x)=-\frac{4}{3}x+\frac{7}{3}$, следователно произведението от ъгловите коефициенти на двете функции трябва да бъде равно на $-1$ т.е. $k.\left(-\frac{4}{3}\right)=-1$, следователно $k=\frac{3}{4}$. Така търсената функция за момента има вида $f(x)=\frac{3}{4}x+n$. За да намерим $n$ ще използваме факта, че графиката й минава през точката $A(-6;-1)$. Заместваме $x=-6$ и $y=-1$, така получаваме $-1=\frac{3}{4}(-6)+n$. Последното равенство можем да разгледаме, като уравнение, в което неизвестното е $n$. Така след като го решим получаваме, че $n=\frac{7}{2}$. Следователно търсената функция е $f(x)=\frac{3}{4}x+\frac{7}{2}$.

5 Задача Намерете линейна функция, графиката, на която минава през точките $A(3;-4)$ и $B(-7;2)$.

Решение: Търсим функция от вида $y=kx+n$. Тъй като графиката й минава през двете точки $A$ и $B$ следва, че са изпълнени равенствата $-4=3k+n$ (заместваме във функцията $x=3$ и $y=-4$) и $2=-7k+n$ (заместваме във функцията $x=-7$ и $y=2$). Забелязваме, че от първото уравнение можем да запишем, че $n=-4-3k$. Сега заместваме $n$ във второто уравнение с $-4-3k$ и получаваме, че $2=-7k-4-3k$. Последното е уравнение с едно неизвестно, което можем да решим. Получаваме, че $10k=-6$ от където $k=-\frac{3}{5}$. Тогава за $n$ имаме, че $n=-4-3\left(-\frac{3}{5}\right)\implies n=-\frac{11}{5}$. Тогава търсената функция има вида $y=-\frac{3}{5}-\frac{11}{5}$.

6 Задача Намерете линейна функция за която е дадено, че $f(0)=5$ и $f(10)=12$.

Решение: Щом са изпълнени тези условия следва, че графиката на линейната функция минава през точките $A(0;5)$ и $B(10;12)$. Търсим функция от вида $y=kx+n$. Заместваме с $x=0$ и $y=5$ от първата точка и получаваме, че $5=0.k+n$ от където веднага намираме, че $n=5$. От втората точка имаме, че $12=10k+n$, но тъй като вече знаем, че $n=5$ можем да запишем уравнението $12=10k+5$ и следователно $k=\frac{7}{10}$. Тогава търсената функция е $f(x)=\frac{7}{10}x+5$.

Задачи за самостоятелна работа:

1. Начертайте графиките на функциите:

а) $f(x)=\frac{1}{2}x+3$; б) $f(x)=2x-1$; в) $f(x)=-\frac{1}{3}+3$; г) $f(x)=-4x-1$.

2. Определете графиките на кои двойки функции са успоредни, перпендикулярни, съвпадащи или нито едно от изброените:

а) $y=5x-5$ и $y=-5x+2$; б) $y=-6x-2$ и $y=\frac{1}{6}x-8$;

в) $y=x-6$ и $y=x+8$; г) $y=2x-8$ и $4x-2y-16=0$.

3. Намерете функция графиката, на която минава през точката $A(5;9)$ и е успоредна с графиката на функцията $y=5x-9$.

4. Намерете функция графиката, на която минава през точката $A(-10;-5)$ и е перпендикулярна с графиката на функцията $6x-5y=24$.

5. Намерете линейна функция графиката, на която минава през точката $A(5;-3)$ и е успоредна на графиката на функцията: 

а) $y=3x-5$; б) $y=-\frac{2}{7}x+\frac{4}{7}$.

6. Намерете линейна функция графиката, на която минава през точките $A(2;4)$ и $B(-1;-5)$.

7. Намерете линейна функция графиката, на която минава през точките $A(0;4)$ и $B(3;4)$.

Още решени и обяснени задачи може да намерите във видеото ми по-долу: