Релации - основни понятия и дефиниции
Определение 1: Нека n е естествено число и M_1, M_2,\ldots M_n e фамилия от множества.
Всяко подмножество R\subseteq M_1\times M_2\times\ldots\times M_n се нарича n-местна релация, а множествата M_1, M_2,\ldots M_n се наричат първи, втори и т.н. n-ти домен на тази релация. Ако вземем n=2 получената релация се нарича двуместна или още бинарна релация.
Ако (m,n)\in R, където R е бинарна релация ще използваме инфиксният запис mRn.
Всяко подмножество R\subseteq M_1\times M_2\times\ldots\times M_n се нарича n-местна релация, а множествата M_1, M_2,\ldots M_n се наричат първи, втори и т.н. n-ти домен на тази релация. Ако вземем n=2 получената релация се нарича двуместна или още бинарна релация.
Ако (m,n)\in R, където R е бинарна релация ще използваме инфиксният запис mRn.
Така от дефиницията ясно се вижда, че ако елементите на едно множество M са в релация с елементите на друго множество N естествено се поражда множеството M\times N, което определя дадената релация.
Съществуват два начина на задаване на релации - конструктивно и дескриптивно. Нека да разгледаме следващият пример.
Пример 1: Нека имаме множествата M=\{10,20,30,40\} и N=\{4,5\}. Разглеждаме следните две бинарни релации, които са зададени дескриптивно:
R_1=\{(m,n)| m\in M, n\in N,\ m\ се\ дели\ на\ n\} и
Съществуват два начина на задаване на релации - конструктивно и дескриптивно. Нека да разгледаме следващият пример.
Пример 1: Нека имаме множествата M=\{10,20,30,40\} и N=\{4,5\}. Разглеждаме следните две бинарни релации, които са зададени дескриптивно:
R_1=\{(m,n)| m\in M, n\in N,\ m\ се\ дели\ на\ n\} и
R_2=\{(m,n)| m\in M, n\in M, m<n \}.
За релацията R_1 получаваме следното множество от наредени двойки:
R_1=\{(10;5), (20;4),(20;5),(30;5),(40;4),(40;5)\}. За всяка наредена двойка, от релацията R_1 е изпълнено условието: "първото число се дели на второто число". Ще казваме, че ралацията R_1 е записана конструктивно чрез явно озброяване на нейните елементи, които са наредени двойки. От тук можем да кажем още и, че R_1\subseteq M\times N
R_1=\{(10;5), (20;4),(20;5),(30;5),(40;4),(40;5)\}. За всяка наредена двойка, от релацията R_1 е изпълнено условието: "първото число се дели на второто число". Ще казваме, че ралацията R_1 е записана конструктивно чрез явно озброяване на нейните елементи, които са наредени двойки. От тук можем да кажем още и, че R_1\subseteq M\times N
За релацията R_2 получаваме следното множество от наредени двойки:
R_2=\{(10;20),(10;30),(10;40),(20;30),(20;40),(30;40)\}. За всяка наредена двойка, от релацията R_2 е изпълнено условието: "първото число е по-малко от второто". И тук релацията R_2 е зададена конструктивно чрез явно изброяване на нейните елементи, които са наредени двойки. От записа на R_2 ясно се вижда, че R_2\subseteq M\times M.
Определение 2: Дефиниционна област или още наричаме домен на релация се нарича множеството D_R=\{x|\ \exists \ y:\ xRy\}, а област от значенията на релация се опредевя от множеството J_R=\{y| \ \exists \ x:\ xRy \}.
Пример 2: Нека имаме множествата M=\{a,b,c,d\} и N=\{1,2,3,4\}. Разглеждаме следната релация R\subset M\times N, като R=\{(a;1), (b;3), (b;4), (c;1)\}. Тогава според Дефиниция 2 D_R=\{a,b,c\}, а J_R=\{1,3,4\}.
За изобразяването на релации можем да използваме няколко метода. Те могат да се предстяват, чрез таблици (матрици), диаграми и графи. Табличното и диаграмно представяне ни дават възможност да представим релации върху две произволни множества, докато представянето с граф ни ограничава само за релации, дефинирани върху едно и също множество.
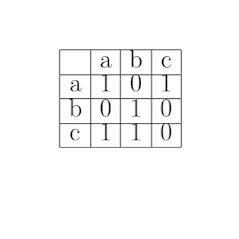
Пример 3: Нека имаме множеството K=\{a,b,c\} и R=\{(a;a), (a;c), (b;b), (c;a), (c;b)\}. Ще представим тази релация таблично по следният начин:
Пример 3: Нека имаме множеството K=\{a,b,c\} и R=\{(a;a), (a;c), (b;b), (c;a), (c;b)\}. Ще представим тази релация таблично по следният начин:
Тъй като в множеството R имаме наредена двойка (a;a) то съответно в клетката, където се пресичат a по хоризонталата и вертикалата пишем единица. Както забелязваме тъй като в R нямаме наредена двойка (a;b) тогава в клетката, която съответства на тази наредена двойка записваме нула. Тъй като в R имаме наредената двойка (a;c) в съответната клетка на таблицата записваме единица. Същото правим и за всяка една от останалите наредени двойки в R.
Определение 3: Обратна релация на релацията R се нарича множеството R^{-1}=\{(n;m)| (m;n)\in R\}.
Като вземем в предвид Определение 2 и Определение 3 можем да кажем, че дефиниционната област на обратната релация R^{-1} се явява областта от стойности на релацията R, а областта от стойностите на R^{-1} е дефиниционната областа на релацията R.
Освен това, лесно се съобразява и, че (R^{-1})^{-1}=R.
Определение 4: Ще казваме, че две релации са равни, ако те се състоят от едни и същи елементи (наредените двойки и в двете релации са едни и същи).
Тъй като релациите са множества, то за тях са в сила операциите с множества - обединение, сечение, разлика, допълнение.
Пример 4: Нека са дадени следните две релации R_1={(a;a), (b;b), (c;c), (a;c)} и R_2={(a;a), (a;b); (b;b), (a;c), (b;c)}. Както беше посочено по-горе за релациите са в сила операцията с множества, тогава следва, че:
R_1\cup R_2=\{(a;a),(b;b),(c;c),(a;c),(a;b),(b;c)\};
R_1\cup R_2=\{(a;a),(b;b),(c;c),(a;c),(a;b),(b;c)\};
R_1\cap R_2=\{(a;a), (b;b), (a;c)\};
R_1\setminus R_2=\{(c;c)\};
R_2\setminus R_1=\{(a;b),(a;c)\}.
Определение 5: Композиция на релациите R_1\subseteq M\times N и R_2=N\times K се нарича релацията R\subseteq <M\times K, такава, че R\{(m;k)|\exists n\in N:(m;n)\in R_1, (n;k)\in R_2\}. Композицията на двете релации R_1 и R_2 ще бележим с R_1\circ R_2.
Доказва се, че композицията на релации не е комутативна, но е асоциативна операция, т.е. R_1\circ R_2\neq R_2\circ R_1 и R_1\circ (R_2\circ R_3)=(R_1\circ R_2)\circ R_3.
Доказва се, че композицията на релации не е комутативна, но е асоциативна операция, т.е. R_1\circ R_2\neq R_2\circ R_1 и R_1\circ (R_2\circ R_3)=(R_1\circ R_2)\circ R_3.
Пример 5: Нека имаме множествата M=\{a,b,c\}, N=\{1,2\} и K=\{d,e,f,g,h\}. Нека освен това за тези множества имаме следните релации R_1\subseteq M\times N и R_2\subseteq N\times K, като R_1=\{(a;1), (a;2), (b;1), (c;2)\} и R_2=\{(1;d),(1;e),(2;f),(2;g),(2;h)\}. Тъй като (a;1)\in R_1 и (1;d)\in R_2 следва, че (a;d)\in R_1\circ R_2, освен това от (a;2)\in R_1 и (2;f)\in R_2 следва, че (a;f)\in R_1\circ R_2 и т.н.
Пример 6: Нека имаме множествата A=\{котка, куче, хаместер\}, B=\{храна, вода\} и C=\{ пакост, наводнение, счупен прозорец, топка\} и следните релации R_1\subseteq A\times B и R_2\subseteq B\times C зададени по следният начин:
R_1=\{(котка;храна), (котка;вода), (куче;храна), (хамстер;вода)\} и R_2=\{(храна;пакост), (храна; топка), (вода; наводнение)\}, тогава от (котка;храна)\in R_1 и (храна;пакост)\in R_2 следва, че (котка;пакост)\in R_1\circ R_2, от (котка;вода)\in R_1 и (вода; наводнение)\in R_2 следва, че (котка;наводнение)\in R_1\circ R_2 и т.н.
Пример 6: Нека имаме множествата A=\{котка, куче, хаместер\}, B=\{храна, вода\} и C=\{ пакост, наводнение, счупен прозорец, топка\} и следните релации R_1\subseteq A\times B и R_2\subseteq B\times C зададени по следният начин:
R_1=\{(котка;храна), (котка;вода), (куче;храна), (хамстер;вода)\} и R_2=\{(храна;пакост), (храна; топка), (вода; наводнение)\}, тогава от (котка;храна)\in R_1 и (храна;пакост)\in R_2 следва, че (котка;пакост)\in R_1\circ R_2, от (котка;вода)\in R_1 и (вода; наводнение)\in R_2 следва, че (котка;наводнение)\in R_1\circ R_2 и т.н.
Задачи за самостоятелна работа:
1. Дадена е двучленната релация R от A=\{a,b,c,d\} в B=\{1,2,3,4,5\} и R=\{(a;1), (a;2). (b;3), (c;4), (d;5)\}. Задайте релацията с таблица.
2. Дадени са релациите R_1=\{(1;4), (1;5), (3;4)\}, R_1\subseteq A\times B и R_2=\{(4;6), (4;7), (5;8), (5;9)\}, R_2\subseteq B\times C над A=\{1,2,3\}, B=\{4,5\} и C=\{6,7,8,9\}. Намерете броя на елементите на композицията R_1\circ R_2.
Използвана литература:



Коментари
Публикуване на коментар