Умножение на вектор с число 8 клас
Преди да разгледаме задачите от този урок ще припомним някои свойства на умножението на вектор с число.
Произведението на вектора \vec{a} с числото \lambda е нов вектор \vec{b}, които:
1) |\vec{b}|=|\lambda|.|\vec{a}|;
2) \vec{b} и \vec{a} са еднопосочни при \vec{a}\neq\vec{0} и \lambda>0, \vec{b} и \vec{a} са разнопосочни при \overrightarrow{a}\neq\overrightarrow{0} и \lambda<0.
Когато \lambda=0 или \vec{0}, тогава \vec{\lambda a}=\vec{0}.
Следствие 1: За ненулевите вектори \vec{AB} и \vec{CD} съществува число \lambda\neq 0 така, че \vec{AB}=\lambda\vec{CD} тогава и само тогава, когато \vec{AB} и \overrightarrow{CD} лежат върху една права или върху успоредни прави.
Следствие 2: Точките O, A и B лежат на една права точно тогава, когато съществува число \lambda такова, че \vec{OA}=\lambda\vec{OB}.
Свойства на произведението на вектор с число:
1) \lambda(\vec{a}+\vec{b})=\lambda\vec{a}+\lambda\vec{b};
2) (\lambda+\mu)\vec{a}=\lambda\vec{a}+\mu\vec{a};
3) 1.\vec{a}=\vec{a};
4) \lambda(\mu\vec{a})=(\lambda\mu)\vec{a}.
Основна задача: Ако O е произволна точка, то точка M е среда на отсечката AB точно тогава, когато \vec{OM}=\frac{1}{2}(\vec{OA}+\vec{OB}).
1 Задача Опростете израза:
а) 7\vec{a}-2(\vec{a}-0,5\vec{b})-3,5\vec{b};
б) 2\vec{a}+\frac{1}{2}(\vec{a}+\vec{b})+\frac{3}{2}(3\vec{a}+\vec{b}).
Решение:
а) 7\vec{a}-2(\vec{a}-0,5\vec{b})-3,5\vec{b}=7\vec{a}-2\vec{a}+\vec{b}-3,5\vec{b}=5\vec{a}-2,5\vec{b}.
б) 2\vec{a}+\frac{1}{2}(\vec{a}+\vec{b})+\frac{3}{2}(3\vec{a}+\vec{b})=2\vec{a}+\frac{1}{2}\vec{a}+\frac{1}{2}\vec{b}+\frac{9}{2}\vec{a}+\frac{3}{2}\vec{b}=
=2\vec{a}+\frac{1}{2}\vec{a}+\frac{9}{2}\vec{a}+\frac{1}{2}\vec{b}+\frac{3}{2}\vec{b}=2\vec{a}+\frac{10}{2}\vec{a}+\frac{4}{2}\vec{b}=2\vec{a}+5\vec{a}+2\vec{b}=
=7\vec{a}+2\vec{b}.
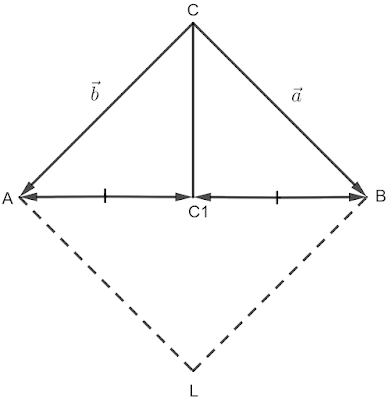
2 Задача Нека е даден \triangle ABC, за който \vec{CB}=\vec{a} и \vec{CA}=\vec{b}. Ако CC_1 е медиана в \triangle ABC, то изразете чрез векторите \vec{a} и \vec{b} векторите:
а) \vec{AB}; б) \vec{BC_1}.
Решение:
а)
Нека да допълним \triangle ABC до успоредника ALBC. От правилото на успоредника (виж събирането и изваждането на вектори и по-специално правилото на успоредника) ясно виждаме, че \vec{AB}=\vec{CB}-\vec{CA}=\vec{a}-\vec{b}, от където исканото в тази подточка е направено.
Нека да допълним \triangle ABC до успоредника ALBC. От правилото на успоредника (виж събирането и изваждането на вектори и по-специално правилото на успоредника) ясно виждаме, че \vec{AB}=\vec{CB}-\vec{CA}=\vec{a}-\vec{b}, от където исканото в тази подточка е направено.
б) Тъй като \vec{AC_1}=\vec{C_1B}=\frac{1}{2}\vec{AB}, следва че \vec{BC_1}=-\frac{1}{2}\vec{AB} от където получаваме, че \vec{BC_1}=\frac{1}{2}(\vec{b}-\vec{a}).
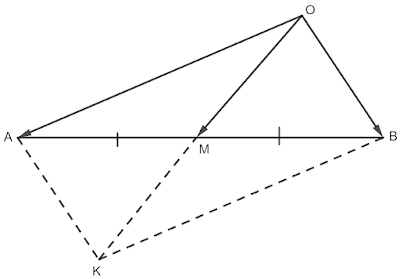
3 Задача Ако точката M е среда на отсечката AB и точката O е произволна точка, докажете, че \vec{OM}=\frac{1}{2}(\vec{OA}+\vec{OB}).
Решение:
Допълваме \triangle ABO до успоредника AKBO. Тъй като M е среда на AB и AB е диагонал на успоредника AKBO то следва, че OK също е диагонал и освен това \vec{OK}=\vec{OA}+\vec{OB}, а \vec{OM}=\frac{1}{2}OK. Следователно \vec{OM}=\frac{\vec{OA}+\vec{OB}}{2}=\frac{1}{2}(\vec{OA}+\vec{OB})
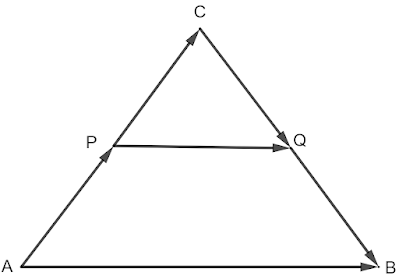
4 Задача Ако P и Q са среди съответно на страните AC и BC на \triangle ABC да се докаже, че \vec{PQ}=\frac{1}{2}\vec{AB}.
Решение:
Тъй като точката P и Q са среди на AC и BC имаме, че \vec{AP}=\vec{PC} и \vec{CQ}=\vec{QB}. От правилото на триъгълника имаме, че \vec{PC}+\vec{CQ}=\vec{PQ}.
Освен това отново чрез правилото на триъгълника имаме, че \vec{AC}+\vec{CB}=\vec{AB}, следователно 2\vec{PC}+2\vec{CQ}=\vec{AB}, като изнесем 2 пред скоби получаваме, че 2(\vec{PC}+\vec{CQ})=\vec{AB}. Сега делим лявата и дясната страна на последното равенство на 2 и получаваме, че \vec{PC}+\vec{CQ}=\frac{\vec{AB}}{2}, т.е. \vec{PQ}=\frac{\vec{AB}}{2}.
Задачи за самостоятелна работа:
1. Да се опрости изразът:
а) (0,5\vec{a}-\vec{b})+\frac{1}{2}\vec{b}+\vec{c};
б) (\vec{a}+\frac{1}{2}\vec{b}-\vec{c})-(\vec{b}-\vec{c}).
2. Дадени са равните вектори \overrightarrow{AB} и \vec{CD}. Ако O е средата на AD, да се докаже, че \vec{BO}=-\vec{CO}.
3. В триъгълникът ABC точката M е средата на медианата CP, а точката N лежи на страната BC, като CN=\frac{1}{3}BC.
а) Ако \vec{CA}=\vec{a}, \vec{CB}=\vec{b}, да се изразят \vec{AM} и \vec{AN} чрез \vec{a} и \vec{b};
б) Да се докаже, че точките A, M, N лежат на една права.
4. Върху страните AB и AC на \triangle ABC са взети съответно точките P и Q такива, че \vec{AP}=\frac{4}{7}\vec{AB} и \vec{AQ}=\frac{4}{7}\vec{AC}. Докажете, че PQ=\frac{4}{7}BC и PQ\parallel BC.
5. Върху страните AB и AC на \triangle ABC са взети съответно точките C_1 и B_1 такива, че AC_1=\frac{1}{3}AB и AB_1=\frac{3}{5}AC. Отсечките BB_1 и CC_1 се пресичат в точка O. Докажете, че точката O е среда на отсечката CC_1.
6. Даден е произволен четириъгълник ABCD, в който M и N са средите на диагоналите, а P е пресечната им точка. Да се докаже, че \vec{PA}+\vec{PB}+\vec{PC}+\vec{PD}=2(\vec{PM}+\vec{PN}).
7. Даден е трапецът ABCD с основи AB и CD. Да се докаже, че \vec{AB}+\vec{DC}=\vec{DB}-\vec{CA}.
8. Да се докаже, че ако точка C дели страната AB на триъгълника ABD в отношение m:n, т.е. ако AC:CB=m:n, то \vec{DC}=\frac{n\vec{DA}+m\vec{DB}}{m+n}.
9. Нека A_1, B_1 и C_1 са среди съответно на страните BC, CA и AB на триъгълника ABC. Да се докаже, че за произволна точка O е изпълнено равенството \vec{OA_1}+\vec{OB_1}+\vec{OC_1}=\vec{OA}+\vec{OB}+\vec{OC}.
10. Даден е триъгълник ABC и точките M и N, за които \vec{AM}=\frac{1}{n}\vec{AC}, \vec{BN}=\vec{CB} и AB\cap MN=P. В какво отношение точката P дели отсечките AB и MN?
11. Върху отсечката AB са избрани точките M, P и K по такъв начин, че \vec{AM}=\frac{1}{4}\vec{AB}, \vec{AP}=\frac{1}{2}\vec{AB}, \vec{KB}=\vec{AM}. Известно е, че разстоянията от A и B до правата a са съответно 12 cm и 32 cm. Да се намерят разстоянията от M, P и K до правата a.
12. Нека M е произволна точка в равнината на \triangle ABC. Точките A_1, B_1 и C_1 са средите съответно на MA, MB и MC, а точките B_2 и C_2 са такива, че \vec{AB}=2\vec{AB_2} и \vec{AC_2}=0,5\vec{AC}. Да се докаже, че \vec{B_2C_2}+\vec{C_1B_1}=\vec{0} и \triangle AB_2C_2\cong A_1B_1C.
13. Даден е триъгълник ABC и точка M от неговата медиана CC_1, като \vec{CM}=\frac{3}{4}\vec{CC_1}, а точката N лежи на страната CB, като \vec{CN}=\frac{3}{5}\vec{CB}. Ако \vec{CA}=\vec{a} и \vec{CB}=\vec{b}, да се докаже, че:
а) \vec{AM}=\frac{1}{8}(3\vec{b}-\vec{a});
б) \vec{AN}=\frac{1}{5}(3\vec{b}-5\vec{a});
в) \vec{AN}=\frac{8}{5}\vec{AM}.
Да се докаже, че точките A, M и N лежат на една права.
14. Върху страната AB на \triangle ABC е избрана такава точка K, че AK:KB=3:10. Да се изрази векторът \vec{CK} чрез векторите \vec{a}=\vec{CA} и \vec{b}=\vec{CB}.
15. Точките A_1 и B_1 лежат съответно върху страните BC и AC на триъгълника ABC. Отсечките AA_1 и BB_1 се пресичат в точката M, като \frac{AM}{MA_1}=\frac{BM}{MB_1}=\frac{2}{1}. Да се докаже, че \vec{AB}=2\vec{B_1A_1}.
16. В четириъгълника ABCD диагоналите AC и BD се пресичат в точка M. Да се докаже, че ако \vec{MA}+\vec{MB}+\vec{MC}+\vec{MD}=\vec{0}.
Още обяснени и решени задачи свързани с този урок можете да намерите във видеото ми дадено по-долу:



Коментари
Публикуване на коментар