Първи и втори признак за еднаквост на триъгълници 7 клас

Нека разгледаме $\triangle ABC$ и $\triangle A_1B_1C_1$. Очевидно на пръв поглед ни изглеждат едни и същи. В математиката, такива триъгълници ще наричаме еднакви.

Определение 1: Два триъгълника, които имат съответно равни страни и съответно равни ъгли, се наричат еднакви.

Твърдението, че $\triangle ABC$ е еднакъв на $\triangle A_1B_1C_1$ ще означаваме по следният начин $\triangle ABC\cong\triangle A_1B_1C_1.$

Теорема 1 (първи признак за еднаквост): Ако две страни и ъгъл заключен между тях от един триъгълник са съответно равни на две страни и ъгъл заключен мужду тях от друг триъгълник, то двата триъгълника са еднакви.

Теорема 2 (втори признак за еднаквост): Ако страна и двата прилежащи към нея ъгъла на един триъгълник са съответно равни на страна и двата прилежащи към нея ъгъла на друг триъгълник, то двата триъгълника са еднакви.

Определение 2: В два еднакви триъгълника височините, медианите и ъглополовящите през съответните върхове се наричат съответни височини, съответни медиани и съответни ъглополовящи.

1 Задача Отсечките $AB$ и $CD$ се пресичат в общата им среда - точката $O$. Докажете, че $\triangle AOC\cong\triangle BOD$.

Решение:

Разглеждаме $\triangle AOC$ и $\triangle BOD$.

1) $AO=BO$ (точката $O$ е среда на $AB$)

2) $CO=DO$ (точката $O$ е среда на $AB$)

3) $\sphericalangle AOC=\sphericalangle BOD$ (връхни ъгли),

следователно $\triangle AOC\cong\triangle BOD$ по I признак.

Тъй като в условието на задачата е оказано, че точката $O$ е обща среда за отсечките $AB$ и $CD$ следва, че (1) $AO=BO$ и (2) $CO=DO$. Освен това (3) $\sphericalangle AOC=\sphericalangle BOD$, защото са връхни ъгли.

2 Задача В остроъгълния триъгълник $ABC$ височините $AH_1$ и $BH_2$ сключват със страната $AB$ равни ъгли. Докажете, че :

а) $\triangle ABH_2\cong\triangle BAH_1$;

б) $\triangle AH_1C\cong\triangle BH_2C$;

в) $\triangle AOH_2\cong\triangle BOH_1$, където $O$ е пресечната точка на $AH_1$ и $BH_2$.

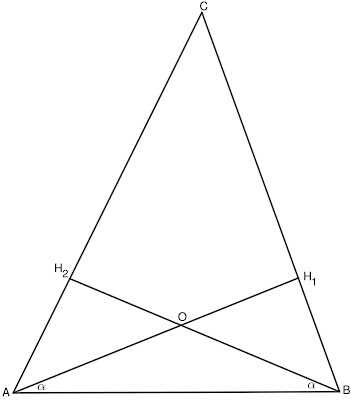
Решение: а) 

Тъй като $AH_1$ и $BH_2$ са височини следва, че $\sphericalangle AH_1B=\sphericalangle AH_1C=90^{\circ}$ и $\sphericalangle BH_2A=\sphericalangle BH_2C=90^{\circ}.$ Следователно за триъгълника $ABH_1$ имаме, че $\sphericalangle ABH_1=90^{\circ}-\alpha$ и аналогично за триъгълника $BAH_2$ имаме, че $\sphericalangle BAH_2=90^{\circ}-\alpha$. Нека тези два факта ги означим с $(1)$.

Разглеждаме триъгълниците $ABH_2$ и $BAH_1$

1) $AB$ - обща

2) $\sphericalangle H_2BA=\sphericalangle H_1AB=\alpha$ (по условие)

3) $\sphericalangle BAH_2=\sphericalangle ABH_1=90^{\circ}-\alpha$ (от (1)), 

следователно от 1), 2) и 3) следва, че $\triangle ABH_2\cong\triangle BAH_1$ по II признак. От това пък, че двата триъгълника са еднакви следва, че $AH_1=BH_2$ и $AH_2=BH_1$.

б) Нека $\sphericalangle C=\gamma$, следователно $\sphericalangle H_1AC=90^{\circ}-\gamma$ и $\sphericalangle H_2BC=90^{\circ}-\gamma$. Нека тези разсъждения означим с (2) Сега разглеждаме  $\triangle AH_1C$ и $\triangle BH_2C$

1) $\sphericalangle AH_1C=\sphericalangle BH_2C=90^{\circ}$ ($AH_1$ и $BH_2$ са височини)

2) $\sphericalangle H_1AC=\sphericalangle H_2BC=90^{\circ}-\gamma$ (от (2))

3) $AH_1=BH_2$ (от подточка а)),

следователно  $\triangle AH_1C\cong\triangle BH_2C$ по II признак от където пък получаваме, че $CH_1=CH_2$, $AC=BC$.

в) Разглеждаме $\triangle AOH_2$ и $\triangle BOH_1$

1) $AH_2=BH_1$ (от подточка а))

2) $\sphericalangle H_2AO=\sphericalangle H_1BO$ (от подточка б))

3) $\sphericalangle AH_2O=\sphericalangle BH_1O=90^{\circ}$ ($AH_1$ и $BH_2$ са височини), следователно $\triangle AOH_2\cong\triangle BOH_1$ по II признак. 

3 Задача В четириъгълника $ABCD$ диагоналът $AC$ е ъглополовяща на $\sphericalangle BAD$ и на $\sphericalangle BCD$.

а) Докажете, че $\triangle ABC\cong\triangle ADC$.

б) Ако периметърът на $ABCD$ е $26$ $cm$ и $AC=10$ $cm$, намерете периметъра на $\triangle ABC$.

Решение:

а) Нека $\sphericalangle BAD=\alpha$ и $\sphericalangle BCD=\beta$, следва, че $\sphericalangle DAC=\sphericalangle CAB=\frac{\alpha}{2}$ и $\sphericalangle DCA=\sphericalangle ACB=\frac{\beta}{2}$.

Разглеждаме $\triangle ACD$ и $\triangle ABC$

1) $\sphericalangle DAC=\sphericalangle BAC=\frac{\alpha}{2}$;

2) $\sphericalangle DCA=\sphericalangle ACB=\frac{\beta}{2}$;

3) $AC$ - обща. 

Следователно от 1), 2) и 3) $\triangle ACD\cong\triangle ABC$ по $II$ признак.

б) От $\triangle ACD\cong\triangle ABC$ $\implies$ $BC=DC$ и $AD=AB$. За периметъра на четириъгълника имаме, че $P_{ABCD}=AB+BC+CD+AD=2AB+2BC$ т.е. $26=2(AB+BC)$ от където намираме, че $AB+BC=13$ $cm$. Така за периметъра на триъгълника $ABC$ получаваме, че $P_{\triangle ABC}=AB+BC+AC=13+10=23$ $cm$.

Задачи за самостоятелна работа

1. За $\triangle ABC$ и $\triangle A_1B_1C_1$ е дадено, че медианите $CM$ и $C_1M_1$ са равни. Ако $AB=A_1B_1$ и $AC=A_1C_1$, докажете, че:

а) $\triangle AMC\cong\triangle A_1M_1C_1$; б) $\triangle ABC\cong\triangle A_1B_1C_1$

2. Дадени са еднаквите $\triangle ABC$ и $\triangle A_1B_1C_1$. Точките $D$ и $D_1$ са средите на страните $AB$ и $A_1B_1$. Да се докаже, че $\triangle ADC\cong\triangle A_1D_1C_1.$

3. Нека $BL$ и $B_1L_1$ са ъглополовящи съответно в $\triangle ABC$ и $\triangle A_1B_1C_1$. Докажете, че ако $\triangle ABC\cong\triangle A_1B_1C_1$, то $BL=B_1L_1.$

Още обяснени и решени задачи свързани с този урок можете да намерите в клипа ми даден по-долу:

Използвана литература:

1. Сборник за 7 клас, Пенка Рангелова, Константин Бекриев, Лилия Дилкина, Нина Иванова изд. Коала Прес, Пловдив, 2020

2. Тест Математика 7 клас, Донка Гълъбова, Адриана Хаджийска, Анна Аначкова и др., изд. Веди, София, 2020 

3. Сборник задачи по математика за 7 клас, Мария Лилкова, Пенка Нинова, Таня Стоева и др., изд. Просвета, София

4. Книга за ученика за 7 клас, Здравка Паскалева, Мая Алашка, Райна Алашка, изд. Архимед, София, 2018

5. Текуща подготовка по математика за наицоналното външно оценяване в 7 клас, Боянка Савова, Мария Тодорова, Веселин Златилов, изд. Просвета, София, 2020

6. Нови пробни изпити за външно оценяване и кандидатстване след 7 клас, изд. Регалия 6, София 2015 

7. Тестове по математика, Любомир Любенов, Цеца Байчева, изд. DOMINO, 2017

8. Нови тематични и общи тестове по математика за 7 клас, Марина Рангелова, изд. Коала Прес, 2008

9. Учебно помагало за задължително избираема подготовка по математика за 7 клас, Иван Тонов, Таня Тонова, изд. Просвета, София, 2011

10. Тестове по математика за 7 клас, Лилия Дилкина, Константин Бекриев, изд. Коала Прес, Пловдив, 2014

11. Сборник контролни работи и тестове по математика 7 клас, Пенка Рангелова, изд. Коала Прес, Пловдив, 2009

12. Сп. Математика

13. Сп. Математика +