Равнобедрен триъгълник. Равностранен триъгълник 7 клас

Определение 1: Триъгълник, на който две от страните са равни се нарича равнобедрен.

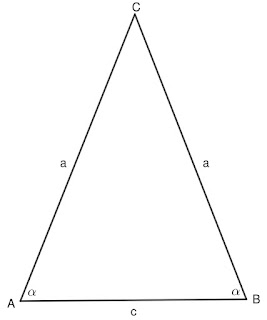
$\triangle ABC$ е равнобедрен триъгълник и $AC=BC=a$. Страните $AC$ и $BC$ се наричат бедра на триъгълника, а страната $AB$ се нарича основа.

Теорема 1: Ако в един триъгълник два от ъглите са равни, той е равнобедрен.

Теорема 2: В равнобедрен триъгълник ъглите при основата му са равни.

Определение 2: Триъгълник, на който и трите страни са равни, се нарича равностранен.

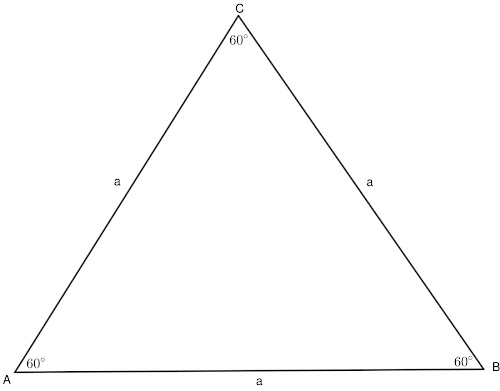
Теорема 3: Ако в триъгълник трите ъгъла са равни, той е равностранен.

Теорема 4: В равностранен триъгълник и трите ъгъла са равни на $60^{\circ}.$

1 Задача: Докажете, че в равнобедрен триъгълник медианите към бедрата са равни.

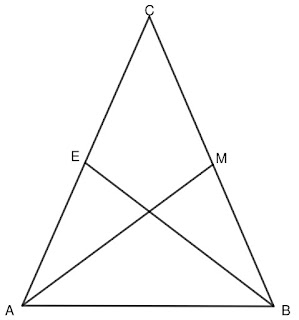
Решение: Нека е даден равнобедреният триъгълник $ABC$ и $AC=BC$. Тъй като $AM$ и $BE$ са медиани следва, че $AE=BM$ (1). От Теорема 2 имаме, че $\sphericalangle BAC=\sphericalangle ABC$ (2).

Разглеждаме $\triangle ABM$ и $\triangle BAE$:

1) $AB$ - обща;

2) $AE=BM$ - от разсъждение (1);

3) $\sphericalangle BAC=\sphericalangle ABC$ - от разсъждение (2).

Следователно триъгълниците $ABM$ и $BAE$ са еднакви по I признак. От това пък, че са еднакви следва, че съответните им страни и ъгли са равни, от където получаваме и, че $AM=BE$ т.е. доказахме, че медианите към бедрата са равни.

2 Задача: В равнобедрен триъгълник ъглополовящата към бедрото е равна на основата. Намерете ъглите му.

Решение: Нека е даден равнобедреният триъгълник $ABC$, в който $AC=BC$ и $AL$ е ъглополовяща на $\sphericalangle BAC$, следователно $\sphericalangle CAL=\sphericalangle LAB=\alpha$ и $\sphericalangle BAC=2\alpha$.

От факта, че $\triangle ABC$ е равнобедрен, според Теорема 2 имаме, че $\sphericalangle BAC=\sphericalangle ABC=2\alpha.$ Тъй като по условие имаме, че $AL=AB$ следва, че $\triangle ABL$ е равнобедрен и отново според Теорема 2 за този триъгълник имаме, че $\sphericalangle ALB=\sphericalangle ABL=2\alpha.$

Така за $\triangle ABL$ имаме, че $\sphericalangle LAB+\sphericalangle ALB+\sphericalangle ABL=180^{\circ}$, от където $\alpha+2\alpha+2\alpha=180^{\circ}$. Така получаваме, че $5\alpha=180^{\circ}$ и $\alpha=36^{\circ}$.

Така за ъглите на $\triangle ABC$ имаме, че $\sphericalangle BAC=\sphericalangle ABC=72^{\circ}$ и $\sphericalangle ACB=180^{\circ}-144^{\circ}=36^{\circ}$, с което задачата е решена.

3 Задача: Даден е равнобедрен триъгълник $ABC$, в който $AC=BC$. Отсечката $BM$ е медиана ($M\in AC$). Ако $BC+CM=15$ $cm$ и $AB+AM=10$ $cm$, намерете страните на $\triangle ABC$.

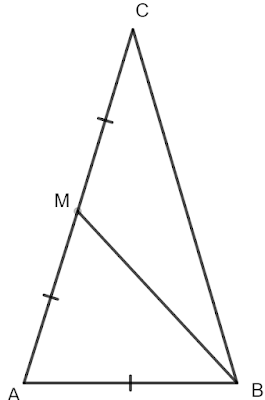
Решение: Нека означим $CM=x$ следователно, тъй като $BM$ е медиана, то и $AM=x$. Тогава $AC=BC=2x$.

Равенството $BC+CM=15$ $cm$ можем да запишем във вида $2x+x=15$ $\implies$ $3x=15$ и $x=5$ $cm$. Така намираме, че $AC=BC=10$ $cm$ и $CM=AM=5$ $cm$.

Сега намираме и $AB$ от равенството $AB+AM=10$ $cm$ следва, че $AB=10-5=5$ $cm$.

4 Задача: В равнобедрения $\triangle ABC$ ($AC=BC$) $\sphericalangle ACB=140^{\circ}$. Точките $K$, $M$ и $P$ са съответно върху страните $AB$, $BC$ и $AC$. Ако $AK=BM$ и $AP=KB$, намерете на колко градуса е равен $\sphericalangle PKM$.

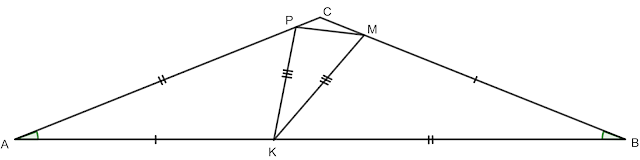
Решение: Построяваме $PK$ и $KM$.

Разглеждаме $\triangle AKP$ и $\triangle BKM$:

1) $AK=MB$ (по условие)

2) $AP=KB$ (по условие)

3) $\sphericalangle PAK=\sphericalangle MBK$ ($\triangle ABC$ - равнобедрен)

$\implies$ $\triangle AKP\cong\triangle BKM$ по $I$ признак $\implies$ $PK=KM$ и $\triangle PKM$ е равнобедрен.

От това, че $\triangle ABC$ е равнобедрен и $\sphericalangle ACB=140^{\circ}$ следва, че $\sphericalangle BAC=\sphericalangle ABC=20^{\circ}$.

Нека означим $\sphericalangle AKC=\alpha$ следователно от $\triangle AKP$, като приложим теоремата за сбор на ъгли в триъгълник имаме, че $\sphericalangle APK=180^{\circ}-(20^{\circ}+\alpha)=160^{\circ}-\alpha=\sphericalangle MKB$.

От това, че $\triangle MKP$ - равнобедрен $\implies$ $\sphericalangle KPM=\sphericalangle PMK=\beta$ $\implies$ $\sphericalangle PKM=180^{\circ}-2\beta$.

Сега вземаме в предвид, че $\sphericalangle AKC+\sphericalangle CKM+\sphericalangle MKB=180^{\circ}$ $\implies$ $\alpha+180^{\circ}-2\beta+160^{\circ}-\alpha=180^{\circ}$ $\implies$ $2\beta=160^{\circ}$. От тук намираме, че $\beta=80^{\circ}$, тогава $\sphericalangle PKM=180^{\circ}-2\beta=180^{\circ}-160^{\circ}=20^{\circ}$.

5 Задача: Даден е $\triangle ABC$ с $\sphericalangle ABC=46^{\circ}$. Ако $CH$ ($H\in AB$) е височина и $AH=BC+BH$, намерете мярката на $\sphericalangle BAC$.

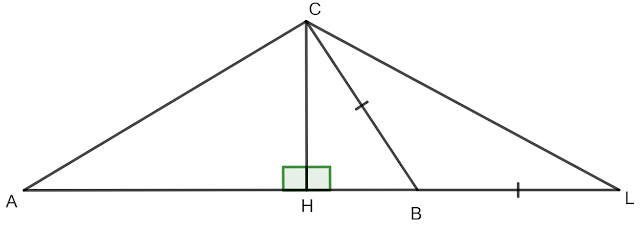
Решение: Построяваме $BL$, така че $BL=BC$. От $AH=BC+BH$ следва, че $AH=HB+BL=LH$.

Тъй като $\sphericalangle CBL$ е съседен на $\sphericalangle ABC$ $\implies$ $\sphericalangle CBL=180^{\circ}-46^{\circ}=134^{\circ}$. От това, че $\triangle LBC$ е равнобедрен $\implies$ $\sphericalangle BLC=\sphericalangle BCL=\frac{180^{\circ}-134^{\circ}}{2}=23^{\circ}$.

Разглеждаме $\triangle AHC$ и $LHC$:

1) $CH$ - обща

2) $\sphericalangle AHC=\sphericalangle LHC=90^{\circ}$

3) $AH=LH$

$\implies$ $\triangle AHC\cong\triangle LHC$ по $I$ признак, а от това, че двата триъгълника са еднакви имаме, че $AC=LC$ и $\triangle ALC$ е равнобедрен $\implies$ $\sphericalangle LAC=23^{\circ}$.

6 Задача: Докажете, че ако външният ъгъл при върха $C$ е два пъти по-голям от $\sphericalangle BAC$ то $\triangle ABC$ е равнобедрен.

Решение: Нека $\sphericalangle BAC=\alpha$, следователно $\sphericalangle BCK=2\alpha$. Тъй като $\sphericalangle BCK$ е външен ъгъл за триъгълника $ABC$, то $\sphericalangle BCK=\sphericalangle BAC+\sphericalangle ABC$ (прилагаме теоремата за външни ъгли, която гласи, че всеки външен ъгъл на триъгълник е равен на сбора от двата не съседни на него вътрешни ъгли) $\implies$ $2\alpha=\alpha+\sphericalangle ABC$ и $\sphericalangle ABC=\alpha$, следователно $\sphericalangle CAB=\sphericalangle ABC=\alpha$. Така доказахме, че $\triangle ABC$ е равнобедрен.

Задачи за самостоятелна работа

1. Докажете, че ако един от ъглите в равнобедрен триъгълник има градусна мярка $60^{\circ}$, то този триъгълник е равностранен.

2. Докажете, че в равнобедрен триъгълник ъглополовящите на ъглите при основата са равни.

3. Докажете, че ако ъглополовящата на един от ъглите на триъгълник разполовява неговия периметър, то триъгълникът е равнобедрен.

4. Страната $AB$ на $\triangle ABC$ е разделена от точките $M$ и $N$ на три равни части, като точка $M$ е между $A$ и $N$. Ако е известно, че $\sphericalangle ACM=15^{\circ}$ и $\sphericalangle CMB=60^{\circ}$, да се намерят ъглите на $\triangle ABC$.

5. Даден е равнобедрен триъгълник $ABC$, за който ъглополовящата на външния ъгъл при върха $B$ образува при пресичането си с правата $AC$ ъгъл, равен на $15^{\circ}$. Намерете градусните мерки на ъглите на $\triangle ABC$.

6. Даден е равностранен $\triangle ABC$. Върху продължението на $AC$ след точка $C$ е взета точката $D$, а върху продължението на $BC$ след точка $C$ е взета точката $E$ така, че $BD=DE$. Докажете, че $AD=CE$.

Видео уроци

Още обяснени и решени задачи свързани с този урок можете да намерите в клипа ми даден по-долу:

Използвана литература:

1. Сборник за 7 клас, Пенка Рангелова, Константин Бекриев, Лилия Дилкина, Нина Иванова изд. Коала Прес, Пловдив, 2020

2. Тест Математика 7 клас, Донка Гълъбова, Адриана Хаджийска, Анна Аначкова и др., изд. Веди, София, 2020

3. Сборник задачи по математика за 7 клас, Мария Лилкова, Пенка Нинова, Таня Стоева и др., изд. Просвета, София

4. Книга за ученика за 7 клас, Здравка Паскалева, Мая Алашка, Райна Алашка, изд. Архимед, София, 2018

5. Текуща подготовка по математика за националното външно оценяване в 7 клас, Боянка Савова, Мария Тодорова, Веселин Златилов, изд. Просвета, София, 2020

6. Нови пробни изпити за външно оценяване и кандидатстване след 7 клас, изд. Регалия 6, София 2015

7. Тестове по математика, Любомир Любенов, Цеца Байчева, изд. DOMINO, 2017

8. Нови тематични и общи тестове по математика за 7 клас, Марина Рангелова, изд. Коала Прес, 2008

9. Учебно помагало за задължително избираема подготовка по математика за 7 клас, Иван Тонов, Таня Тонова, изд. Просвета, София, 2011

10. Тестове по математика за 7 клас, Лилия Дилкина, Константин Бекриев, изд. Коала Прес, Пловдив, 2014

11. Сборник контролни работи и тестове по математика 7 клас, Пенка Рангелова, изд. Коала Прес, Пловдив, 2009

12. Сп. Математика

13. Сп. Математика +